Question 612867: Find the two substitutions on the interval [0,2"pi"] 3sinx=sinx-1
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
Solving equations like this usually involve three stages:- Using algebra and/or Trig properties to transform the equation into inot of more equations of the form:
TrigFunction(expression) = number - Find the general solution for the equation(s) from step 1. (Because Trig functions are periodic, they will have an infinite number of solutions: All the angles that terminate in the right quadrant(s) with the right reference angle. The general solution expresses this infinite set of solutions.
- Many problems ask for specific solutions. For example, "find the smallest positive solution to..." or, like your problem, "Find all solutions within the interval ...". If specific solutions are requested, use the general solution from step 2 to find it/them.
Let's see this in action:
1. Transform the equation into the desired form.
With your equation, this is fairly simple. Just subtract sin(x) from each side:
2sin(x) = -1
and divide both sides by 2:
sin(x) = -1/2
This is the desired form.
2. Find the general solution.
We're looking for the angles whose sin ratio is -1/2. First, sin is negative in the 3rd and 4th quadrants so x must terminate in one of those quadrants. Next we determine the reference angle. (Note: Ignore the negative, if any, when determining the reference angle.) We should recognize that a sin ratio of 1/2 is a special angle value. The reference angle whose sin is 1/2 is  . So we're looking for angles that terminate in the 3rd or 4th quadrants whose reference angle is . The general solution will include an equation for each quadrant. For the third quadrant, we add the reference angle to  :
which simplifies to
For the 4th quadrant we can either use the negative of the reference angle or we subtract the reference angle from  . So we can use:
or
which simplifies to:
Either
or
can be used. It does not matter which. I'll pick the first one. This makes the full general solution:
or
Notes:- The "n" in the general solutions equations represents any integer. There are an infinite number of integers. And each one of them will result in a different value for "x". This is how we can express an infinite number of solutions without having to list them individually.
- Some textbooks/teachers use "k" or some other letter instead of "n". The particular letter used makes no difference. No matter what letter is used, it represents integers.
- The "+
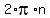 " part of the general solutions equations is how we express the idea of the co-terminal angles. For example, our equation
says that x can be  or any other angle that is co-terminal with .
3. Find the specific solution(s), if requested.
Your problem asks for solutions that are in the interval: [0, ]. To find these we start trying different integers for "n" in each equation until you're satisfied that you have found all the x's that are within the interval.
From the first equation of the general solution:
we should be able to see that if n = 0, then  which is in the desired interval. With a little thought and/or calculation you should be able to figure out that positive n's result in x's that are too big (larger than and that negative n's result in x's that are too small (below 0). So we only get one specific solution from this general solution equation.
From the second equation of the general solution:
we should be able to tell that when n = 0,  which is below 0. Negative n's will result in even lower x's. But n = 1 results in  which is in the desired interval. n's that are 2 and higher will result in x's higher than .
So we end up with two specific solutions in the desired interval:
or
Note: We got one specific solution from each equation of the general solution. Do not depend on this. Sometimes no specific solutions come from a particular equation of the general solution and sometimes you get more than one. Be sure to try different integers for n in each equation of the general solution until you feel you found all the specific solutions.
|
|
|
