Question 527721: using the law of sines, solve for the missing measures.
A=60 degrees
B=
C=
a=9
b=
c=10
so far i have sin60/9 = sinC/10
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! using the law of sines, solve for the missing measures.
A=60 degrees
B=
C=
a=9
b=
c=10
so far i have sin60/9 = sinC/10
This is the AMBIGUOUS case SSA, (side-side-angle) which may have 0 solutions,
1 solution, or 2 solutions. If it has 2 solutions we call them triangle ABC
with sides a,b,c, and triangle A'B'C' with sides a',b',c'.
I'll tell you in advance that there are two solutions to this problem,
The first two figures below show the two solutions, and the third
figure below shows them put together with triangle A'B'C' inside of
triangle ABC, the blue arc shows that a and a' both equal 9 in length:
   First solution Second solution (maybe)
A = 60░ A' = 60░
B = B' =
C = C' =
a = 9 a' = 9
b = b' =
c = 10 c' = 10
We start with what you had:
First solution Second solution (maybe)
A = 60░ A' = 60░
B = B' =
C = C' =
a = 9 a' = 9
b = b' =
c = 10 c' = 10
We start with what you had:
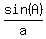 = = 
 = =  9Ěsin(C) = 10Ěsin(60░)
sin(C) =
9Ěsin(C) = 10Ěsin(60░)
sin(C) =  sin(C) = .9622504486 <--- If this had been greater than 1, there
whould have been no solution. If this had
been exactly 1, there would have been 1 right
triangle angle solution. But since it is less \
than 1, we can tell that there is either 1 or 2
solutions.
If you use your calculator with the inverse sine,
you get
C = 74.20683095░.
That is a correct value for angle C. However there is another
possible angle with that same sine, which is a second quadrant
angle, and it is found by subtracting 74.20683095░ from 180░.
We'll call it C':
C' = 180░ - 74.20683095░ = 105.793169░
So we put those two values in:
First solution Second solution (maybe)
A = 60░ A' = 60░
B = B' =
C = 74.20683095░. C' = 105.793169░
a = 9 a' = 9
b = b' =
c = 10 c' = 10
To find out whether there are 2 solutions or only 1,
we calculate the angles B and B', and see if both
are possibilities:
We calculate B by using 180░-A-C = 180░-60░-74.20683095░ = 45.79316905░
We calculate B' by using 180░-A'-C' = 180░-60░-105.793169░ = 14.20683095░
Since B' came out positive, we know that there are two solutions,
[If B' had come out negative, there would have been only 1 solution].
First solution Second solution
A = 60░ A' = 60░
B = 45.79316905░ B' = 14.20683095░
C = 74.20683095░. C' = 105.793169░
a = 9 a' = 9
b = b' =
c = 10 c' = 10
Now we just have to calculate sides b and b'
To calculate side b:
sin(C) = .9622504486 <--- If this had been greater than 1, there
whould have been no solution. If this had
been exactly 1, there would have been 1 right
triangle angle solution. But since it is less \
than 1, we can tell that there is either 1 or 2
solutions.
If you use your calculator with the inverse sine,
you get
C = 74.20683095░.
That is a correct value for angle C. However there is another
possible angle with that same sine, which is a second quadrant
angle, and it is found by subtracting 74.20683095░ from 180░.
We'll call it C':
C' = 180░ - 74.20683095░ = 105.793169░
So we put those two values in:
First solution Second solution (maybe)
A = 60░ A' = 60░
B = B' =
C = 74.20683095░. C' = 105.793169░
a = 9 a' = 9
b = b' =
c = 10 c' = 10
To find out whether there are 2 solutions or only 1,
we calculate the angles B and B', and see if both
are possibilities:
We calculate B by using 180░-A-C = 180░-60░-74.20683095░ = 45.79316905░
We calculate B' by using 180░-A'-C' = 180░-60░-105.793169░ = 14.20683095░
Since B' came out positive, we know that there are two solutions,
[If B' had come out negative, there would have been only 1 solution].
First solution Second solution
A = 60░ A' = 60░
B = 45.79316905░ B' = 14.20683095░
C = 74.20683095░. C' = 105.793169░
a = 9 a' = 9
b = b' =
c = 10 c' = 10
Now we just have to calculate sides b and b'
To calculate side b:
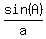 = = 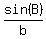
 = =  bĚsin(60░) = 9Ěsin(45.79316905░)
b =
bĚsin(60░) = 9Ěsin(45.79316905░)
b =  b = 7.449489743
---
To calculate side b':
b = 7.449489743
---
To calculate side b':
 = = 
 = =  b'Ěsin(60░) = 9Ěsin(45.79316905░)
b' =
b'Ěsin(60░) = 9Ěsin(45.79316905░)
b' =  b' = 2.550510257
So we end up with:
First solution Second solution
A = 60░ A' = 60░
B = 45.79316905░ B' = 14.20683095░
C = 74.20683095░ C' = 105.793169░
a = 9 a' = 9
b = 7.449489743 b' = 2.550510257
c = 10 c' = 10
Edwin
b' = 2.550510257
So we end up with:
First solution Second solution
A = 60░ A' = 60░
B = 45.79316905░ B' = 14.20683095░
C = 74.20683095░ C' = 105.793169░
a = 9 a' = 9
b = 7.449489743 b' = 2.550510257
c = 10 c' = 10
Edwin
|
|
|