SOLUTION: sin 2x + cos 60 = 0, 0 < x < 360. i have been able to find out that sin inverse of -1/2 is -30, but how do i find answers in the 3rd and fourth quadrant for 2x?? then i can find

Question 488238: sin 2x + cos 60 = 0, 0 < x < 360.
i have been able to find out that sin inverse of -1/2 is -30, but how do i find answers in the 3rd and fourth quadrant for 2x?? then i can find x. my answers are coming wrong, and i can apply no suitable rule. please help, and show working if possible.
Found 2 solutions by stanbon, Theo:
Answer by stanbon(75887) (Show Source): You can put this solution on YOUR website!
sin 2x + cos 60 = 0, 0 < x < 360.
i have been able to find out that sin inverse of -1/2 is -30, but how do i find answers in the 3rd and fourth quadrant for 2x?? then i can find x. my answers are coming wrong, and i can apply no suitable rule. please help, and show working if possible.
-----------------------
sin(2x) + (1/2) = 0
sin(2x) = -1/2
2x = arcsin(-1/2) = 210 or 330
x = 105 or 165 degrees
------------------------------
Note: If you know sin(theta) = 1/2
then sin(180-theta) = 1/2
and sin(180+theta) = -1/2
and sin(360-theta) = -1/2
---
You can find those relationships
on the unit circle.
==========
Cheers,
Stan H.
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
your equation is:
sin (2x) + cos(60) = 0
since cos(60) = 1/2, this equation becomes:
sin (2x) + 1/2 = 0
subtract 1/2 from both sides of this equation to get:
sin (2x) = -(1/2)
the sin is negative in the third and fourth quadrants only.
solve the angle as if it was in the first quadrant.
you get sin(2x) = 1/2
this means that 2x = sin^-1(1/2) which becomes 2x = 30 degrees.
your answer would be 2x = 30 degrees if the angle was in the first quadrant.
the equivalent angle in the third quadrant would be 180 + 2x which would make the angle 210 degrees.
the equivalent in the fourth quadrant would be 360 - 2x which would make the angle 330 degrees.
your original equation becomes:
sin(210) + cos(60) = 0
sin(330) + cos(60) = 0
solve both of these equations using your calculator and you'll see that they are both true.
a picture of what we just did is shown below.

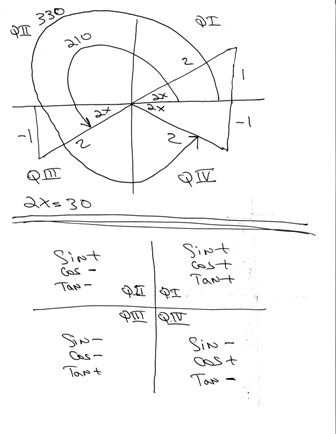
we first solved for the reference angle.
that was the angle in the first quadrant.
we got a positive value because we were in the first quadrant.
we then determined that our value had to be negative.
we had to know that the sine is negative in the third and fourth quadrant only.
we then had to find an equivalent angle in the third and fourth quadrant.
the formula to derive that is as follows:
the reference angle is always in the first quadrant.
if the angle is in the second quadrant, then the angle is equal to 180 minus the reference angle.
if the angle is in the third quadrant, then the angle is equal to 180 plus the reference angle.
if the angle is in the fourth quadrant, then the angle is equal to 360 minus the reference angle.
we found the angle in the third and fourth quadrant because the sine is negative in the third and fourth quadrant.

RELATED QUESTIONS
find all solutions for equation with value of x between 0 and 360 degrees: 1. sin(4x) + (answered by jim_thompson5910)
How to: "Find the number of solutions of the equation cos^2-1=0 in the interval [0, 2pi] (answered by Fombitz)
Dear Math Tutor, Find two values of x between 0 and 360 such that sin x degrees = -... (answered by lwsshak3)
I'm attempting to do corrections on a test, but these three questions are giving me... (answered by stanbon,Edwin McCravy)
It states to find all values of theta in [o,360] that satisfy each equation cos theta... (answered by lwsshak3)
I have 2 questions" 1)Find all values of θ that satisfy the equation over the... (answered by rothauserc)
sin(A+B) = sin A cos B + cos A sin B cos(A+B) =... (answered by vleith)
An explanation to my question would be greatly appreciated. I have many of these... (answered by MathTherapy)
hey, i am doing a exam review packet for my math class. i am having a ton of problems... (answered by user_dude2008)