Question 420692: write an equation of the cos function with an amplitude of 4, period of 6, phase shift -pi, and verticle shift of -5.
Found 2 solutions by lwsshak3, jsmallt9:
Answer by lwsshak3(11628)   (Show Source):
You can put this solution on YOUR website! write an equation of the cos function with an amplitude of 4, period of 6, phase shift -pi, and verticle shift of -5.
..
Basic equation of cos function: y=ACos(Bx-C)
A=amplitude
B=coefficient of x
Period=2pi/B
Phase shift=C/B
..
Given amplitude=4=A
Given Period = 6=2pi/B
B=2pi/6=pi/3
Given phase shift=-pi=C/B
C=B*-pi=(pi/3)*-pi=-pi^2/3
Given vertical shift=-5 (Curve is bumped down 5 units)
..
Equation:
y=4Cos(pi/3x+pi^2/3)-5
Answer by jsmallt9(3758) (Show Source):
You can put this solution on YOUR website! The general form of the cos function that I am familiar with is:
y = A*cos(B(x-D) + C
where
A = amplitude
B = 2pi/period
C = vertical shift
D = phase shift
The letters A, B, C, and D can be different but what is important is the form. For example the number in front of "cos" is the amplitude no matter what letter you use for it. If this form is more like what you were taught than the form used by another tutor in his/her solution, then read on.
You are given the values for A, C and D (the amplitude and the two shifts). We just have to use the given period for calculate the B:
Now that we have all four values we can write the equation:
which will simplify to:
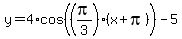
This is the answer in the form I know.
P.S. If you multiply out  you end up with almost the same equation as the solution from the other tutor. (His equation has a "-" in the argument of the cos and it should be "+", like mine). Otherwise the other solution is correct, too. It is in a different form which, IMHO, is harder to find than the form used in this solution. In fact, if I wanted the other form, I would find my form and then distribute the "B".
|
|
|
