Question 36126: find the exact value of tan 30 degrees
Found 2 solutions by stanbon, rapaljer:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! find the exact value of tan 30 degrees
Draw a right triangle with a 30 degree angle
Let the side opposite the 30 degree angle be "1".
Then by geometry we know the hypotenuse is "2"
because " the side opposite the 30 degree angle is
one-half the hypotenuse".
Using Pythagoras you can find the 2rd side, as follows:
1^2 + x^2 = 2^2
x^2=3
x=sqrt 3
Then the tangent is opposite/adjacent = 1/sqrt3 = sqrt3/3
Cheers,
Stan H.
Answer by rapaljer(4671)  (Show Source):
You can put this solution on YOUR website! Construct an equilateral triangle --all angles 60 degrees-- with each side equal to 2, and drop a perpendicular line down the middle of the triangle. This perpendicular line will cut the equilateral triangle into TWO right triangles, and it will cut the base of the equilateral triangle in half. Now, look at the right triangle on the left side and let x = the height of the triangle. Use the Theorem of Pythagoras to solve the right triangle whose legs are 1 and x, and the hypotenuse is 2.
Now, since the angle at the top, which was 60 degrees was cut in half by the perpendicular line, that means that this angle in the right triangle is 30 degrees. Remember that  . In this triangle from the 30 degree angle, the opposite side is 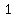 , and the adjacent side is  , so  .
Now that I did all this work explaining how it was derived, maybe you just wanted the answer? If so, skip all the previous explanation, and this is it:
.
R^2 at SCC
|
|
|
