how far is the ship from the lighthouse after 45 minutes.
what is the bearing of the ship to the lighthouse then.
bearing has to do with degrees.
compass degrees start at 0 from due north and increase clockwise until they go around 1 complete revolution.
0 degrees is north
90 degrees is east
180 degrees is south
270 degrees is west
360 degrees is north again.
The ship is traveling west which means that the ship is traveling at a bearing of 270 degrees.
The lighthouse is 10km northwest of the ship at time point 0.
Northwest means the lighthouse is at a bearing of 315 degrees from the ship.
This means that the angle between the direction the ship is going and the lighthouse is 315 - 270 = 45 degrees.
Since the ship is traveling at 16 kmph and has traveled for 45 minutes, then the ship has traveled 45/60 * 16 = 12 km.
We can draw a right triangle as follows:
270 degree bearing horizontal line from the ship due west is one leg of the right triangle.
Vertical line from the horizontal line to the lighthouse is the other end of the right triangle. This vertical line makes a 90 degree angle with the horizontal line.
Line from the lighthouse to the ship is the hypotenuse of this right triangle.
Since the hypotenuse is 10 km, and the angle between the ship and the horizontal line is 45 degrees, then the length of the vertical line is equal to 10 * sin(45) = 7.071067812 km.
We'll call that line y.
y = 7.071067812 km.
The horizontal distance from where the ship is to the vertical line is equal to 10 * cos(45) = 7.071067812 km.
Well call that line x.
The ship has moved 12 km due west.
Since the ship has moved west 12 km, and since the ship was 7.071067812 km from the vertical line, this means that the ship has passed the vertical line and gone 12 - 7.071067812 km = 4.928932188 km further.
The ship now forms another right triangle with the lighthouse.
The vertical distance between the ship and the lighthouse hasn't changed.
That will always be equal to y which is 7.071067812 km.
The actual distance has changed. This is represented by the hypotenuse of the new right triangle that has been formed.
The vertical leg of this new right triangle is 7.071067812 km.
The horizontal leg of this new right triangle is 12 - x = 12 - 7.071067812 = 4.928932188.
We'll call that line z.
If T is the new angle between the ship and the lighthouse, then tan(T) = opp/adj = y/z = 7.071067812 / 4.928932188 = 1.434604402.
arctan (1.434604402) = 55.12133308 degrees.
We let w = the hypotenuse of this new right triangle.
sin(55.12133308) = opp/hyp = y/w = 7.071067812/w.
Multiply both sides of this equation by w and divide both sides of this equation by sin(55.12133308) and you get:
w = 7.071067812/sin(55.12133308).
This makes w = 8.61941834 km.
That's the new distance from the ship to the lighthouse.
The ship is still heading at a bearing of 270 degrees.
The lighthouse, however, is now at a bearing of 90 - 55.12133308 = 34.87866692 degrees from the ship which makes the lighthouse northeast by north from the ship.
A picture of what this looks like is shown below:
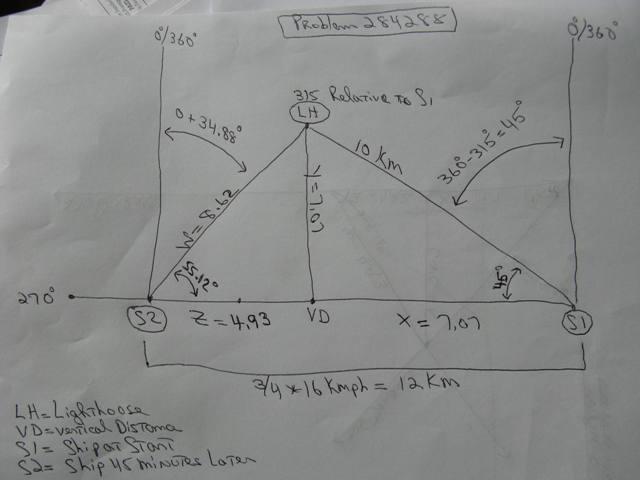
S1 is where the ship is originally.
0/360 degrees on the compass is straight up from there.
LH is where the Lighthouse is.
315 degrees on the compass is 45 degrees to the right of 0 degrees.
Since due west is 270 degrees, that means that the line of travel of the ship is 9 degrees from the 0 mark on the compass, and 45 degrees from the straight line distance between the ship and the lighthouse.
Cos(45) and Sin(45) both equal 7.07.....
This means that the horizontal distance from the ship to the lighthouse and the vertical distance from the ship to the lighthouse are both 7.07.....
In 3/4 of an hour, at 16 km per hour, the ship travels 12 km.
That puts the ship at S2.
The straight line distance of the ship to the Lighthouse now has to be calculated.
Since the ship travels 12 km to get to S2 from S1, and the vertical distance to the Lighthouse is 7.07.... km away, this means that the horizontal distance from the ship at S2 to the vertical distance point of the lighthouse from the same horizontal line is 4.93... km.
Using the tangent formula, we can then find the angle.
If T is the angle at S2, then:
Tan(T) = 7.07... / 4.93 ... = 1.434.....
Arctan(1.434....) = 55.12.... degrees.
From that, we derive the length of W which is equal to either Sin(55.12...) = 7.07... / W, or Cos(55.12...) = 4.93... / W.
The ship at S2 has a bearing of 0 degrees straight up.
55.12... degrees from the horizontal = 34.88... degrees from the vertical which makes the bearing of the Lighthouse from the ship at S2 equal to 34.88... degrees which is equivalent to a bearing of Northeast by North.
A key point is that the compass reading is taken from the ship.
As the ship moves west, the position of the lighthouse on the compass changes relative to the ship.
The position of due north at 0 degrees relative to the ship remains unchanged.
The website where I got the northeast by north designation is at the following link:
Wind Direction Compass Bearings
From that table I got:
Northwest (NW) is between 309.38° and 320.62°
Northeast by North (NEbN) is between 28.13° and 39.37°
Once you get to that website, you have to scroll down a little over halfway to get to the table.