SOLUTION: On one extreme, a circle is a special case for an ellipse; at the other extreme, a ? can be viewed as another special case for an ellipse

When viewed as a circle, both foci and the center of the circle coincide.
The minor and major axes are equal, and are both the same as the radius
of the circle. 

, 



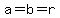which becomes:



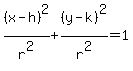or



But it can also be viewed as a line segment where the focal points
coincide with the vertices, and the center is at the midpoint of the
line segment.

However we cannot use the standard form of an ellipse to show its
equation.  We would have to use this alternate form of an ellipse:



where either a or b is zero. If b=0 we have

 with 

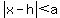
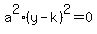 with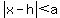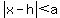 

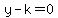 with 

 with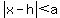 

Notice below, at one extreme we have the outer circle,
then the green ellipse, then the blue ellipse, etc, 
and how the ellipses shrink down to the line segment 
from -2 to +2, at the other extreme:



I'll go through them.  We start with the ROUNDEST
of all ellipses, the circle:



Now let's squash the above circle above down
into this green ellipse:



Next let's squash it some more down to half-size the 
original circle, and we get this blue ellipse:



Next we squash even some more, and get this
purple ellipse:



Keep squashing and we get this grey ellipse,
which as you see is very flat:



Now finally we have squashed it all the way flat, 
we have nothing left but an ellipse which is but a 
flat line segment:



The point here is that the circle is the ROUNDEST ellipse of 
all, and a line segment is the FLATTEST ellipse of all.

If you'll look through the above series of ellipses, you start
with the roundest ellipse of all, the circle, and squash it
down flatter and flatter, and when you squash it all the
way flat, all you have is a flat line segment.  BUT both the
circle we began with and the line segment we ended up with
are BOTH extreme cases of ellipses.

In other words, a circle IS an ellipse and a line segment IS
an ellipse, and all other ellipses are somewhere in between
not being squashed at all, or squashed all the way down into
a line segment. 


Edwin