SOLUTION: find all solutions: cotx-1=cscx; in the interval [0,2pi)

Your equation is

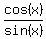     - 1 =   in the interval [0, 2pi).


Notice that sin(x) is in the denominator: it means that the domain of this equation
is the part of the interval [0,2pi), where sin(x) =/= 0.
In other words, the domain is  the union of intervals (0,pi) U (pi,2pi).  
The points  x= 0  and  x= pi  are gouged out.


OK. Multiply both sides by sin(x).  We can do it in the domain, since sin(x) =/= 0 there.
    You will get


    cos(x) - sin(x) = 1.


To solve, square both sides

    cos^2(x) - 2cos(x)*sin(x) + sin^2(x) = 1.


Replace cos^2(x) + sin^2(x) by 1 and cancel 1 in both sides.  You will get

    -2cos(x)*sin(x) = 0.


It means that either cos(x) = 0  or  sin(x) = 0.

But sin(x) = 0 is excluded in the domain;  so, the only possibility to consider is cos(x) = 0.

It gives two solutions for x:  x = pi/2  and  x= 3pi/2.


Check shows that x= pi/2 is an extraneous solution.


ANSWER.  In the given domain, the original equation has a unique solution  x= 3pi/2.