Question 1205013: The graph shows part of a sine function of the form y = A sin B(x + C) + D. Determine the values of A, B, C, and D.
The answer key is A = 2, B = 3, C = -π/3, D = -1
But I am in need of a worked-out solution
Is y = A sin B(x + C) + D the same as y = asin(bx - c) + d? I'm confused. I don't understand why the first formula has "+ C" instead of "- c". I thought the formula of the parent graph is always written "- c" regardless if the value of c is negative or positive. I understood that only after replacing the variables with values and if "c" has a negative value and you are subtracting a negative (double negatives) that it becomes addition, but why is the first formula with variables "+ C" instead of "- c"? And why is "B" outside the parenthesis instead of inside? I thought "b" was supposed to be a quotient of "x".
Found 4 solutions by math_tutor2020, MathLover1, ikleyn, greenestamps:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Many teachers and textbooks decided that sin x is fine when others prefer sin(x) to make it more clear what the input argument is.
The second version leads to more parenthesis but it's worth it I think.
Something like sin B(x + C) is the same as sin( B(x + C) ) to tell the reader "The B(x+C) part is inside the sine function".
It's a bit confusing I know.
No, y = A sin B(x + C) + D is NOT the same as y = A*sin(Bx - C) + D; however, the two are somewhat similar at least.
The A, B, and D play the exact same role for either template. The C is a bit different.
Here's an example graph showing that y = A sin B(x + C) + D is NOT the same as y = A*sin(Bx - C) + D
https://www.desmos.com/calculator/sbgketg7yy
Check out this page
https://math.libretexts.org/Courses/Rio_Hondo/Math_175%3A_Plane_Trigonometry/02%3A_Graphing_Trigonometric_Functions/2.04%3A_Transformations_Sine_and_Cosine_Functions
to refresh your memory of what each parameter does.
The template that link uses is y = A*sin(Bx - C) + D
However, since your teacher is using the template
y = A*sin(B(x + C)) + D
it's best to stick to it
|A| = amplitude
B = used to determine period
C = used to determine phase shift
D = vertical shift and midline
The highest and lowest points on this sinusoidal curve is when y = 1 and y = -3 respectively.
The midpoint is (max+min)/2 = (1+(-3))/2 = -1 which is the midline. Therefore D = -1
The vertical gap between those y values is 4 units. Count out the spaces. Or subtract and use absolute value. Half of this vertical distance is the amplitude. So either A = 2 or A = -2. Both will work. I'll go with A = 2 for simplicity sake, and to match what your answer key shows (note: if you picked A = -2, then the C value would be different from C = -pi/3 while everything else is the same).
The lowest point occurs when y = -3
Circle two neighboring valley points and record their x values. Two such x values are x = pi/6 and x = 5pi/6
The horizontal gap between them is 5pi/6 - pi/6 = 4pi/6 = 2pi/3
This is the period. It's the length of each cycle. The curve repeats itself every 2pi/3 horizontal x units.
T = period
T = 2pi/B
B = 2pi/T
B = 2pi/( 2pi/3 )
B = 2pi * (3/(2pi))
B = 3
Note how,
T = 2pi/B
T = 2pi/3
So we confirm we have the correct B value.
The last thing to find is the value of C.
So far we have:
A = 2
B = 3
D = -1
Plug those into the template y = A*sin( B(x + C) ) + D and we get y = 2*sin( 3(x + C) ) - 1
Then plug in one of the min or max points on the curve. Let's say we picked (x,y) = (pi/2, 1)
Let's solve for C.
y = 2*sin( 3(x + C) ) - 1
1 = 2*sin( 3(pi/2 + C) ) - 1
1 + 1 = 2*sin( 3(pi/2 + C) )
2 = 2*sin( 3(pi/2 + C) )
2/2 = sin( 3(pi/2 + C) )
1 = sin( 3(pi/2 + C) )
3(pi/2 + C) = arcsin(1)
3(pi/2 + C) = pi/2
3pi/2 + 3C = pi/2
3C = pi/2 - 3pi/2
3C = -2pi/2
3C = -pi
C = -pi/3
Here's a Desmos graph to confirm our answers
https://www.desmos.com/calculator/iosov8wrk1
GeoGebra is another graphing tool I use all the time.
Answer by MathLover1(20849)  (Show Source):
You can put this solution on YOUR website! 
where
 is amplitude (The amplitude of the graph is the maximum height the graph reaches from the x-axis.)
 is period (The period is the distance along the x-axis that is required for the function to make one full oscillation.)
 is phase shift (The phase shift is the measure of how far the graph has shifted horizontally.)
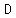 is vertical shift (The vertical shift is the measure of how far the graph has shifted vertically, either up or down, from its initial position.)
here is the graph of parent function 
The graph of has:
- an amplitude of 
- a period of 
- a phase shift of 
- a vertical shift of
you need to compare it to the given graph to determine the values of ,  , , and
as you can see, midline goes through  ( line parallel to  -axis, means the graph is    unit)=> 
the 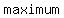 height the graph reaches from the x-axis is from  to ,  units,
the distance from  to  and from to is  units, so the amplitude is
The period of the graph is .
given function makes one full oscillation at 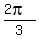 (when you start at point (,) and go to point ( ,))
so, the period is:  => 
the graph has shifted horizontally  to the right, so
the graph has shifted vertically one unit down, so
your equation is:
Is  the same as  ? =>  , it’s not same
reason:
when  is positive the graph shifts to the left
when is negative the graph shifts to the right
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
Hello, other tutors wrote many words, but they did not answer your question.
Look at the plot.
You see sinusoidal periodical curve.
You may move/shift it one period to the right (by subtracting the period from the argument) -
- you will get the same curve, since the function is periodical.
You may move/shift it one period to the left (by adding the period to the argument) -
- you will get the same curve, since the function is periodical.
It explains WHY you may have THE SAME CURVE, even although you have positive argument in one form, but negative argument in other form.
Different formulas for sine function describe THE SAME CURVE, if the arguments differ by integer number of periods.
So, different values of the sine argument may describe (and do describe) the same curve,
if the arguments differ by integer values of periods.
It is common property of all periodic functions : sin(x), cos(x), tan(x), sec(x), csc(x),
 ,  ,  , sin(x)*cos(x),  etc.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
You write in your post:
Is y = A sin B(x + C) + D the same as y = asin(bx - c) + d? I'm confused. I don't understand why the first formula has "+ C" instead of "- c".
It looks as if your confusion is about the "+ C" and the "- c".
In that case, you probably didn't write the two forms of the formula correctly.
(I am also concerned about your use of capital letters in one form and lower case letters in the other form. I hope you aren't using a resource that uses capital letters if the form has "+ C" and lower case letters if the form has "- c". That would be VERY confusing and therefore most unfortunate....)
ASSUMING there is no difference between the forms with capital and lower case letters, it is certainly NOT TRUE that
y = A sin B(x+C) + D
and
y = A(sin(Bx+C) + D
are the same.
The "B" outside the parentheses in one form and inside the parentheses in the other make the two forms very different.
I suspect you meant to write both forms with the "B" outside the parentheses, as the form with it inside the parentheses is much less useful.
So in order to try to help you with this, I am going to assume that the two forms you are looking at are
y = A sin B(x+C) + D
and
y = A sin B(x-C) + D
so that the only difference is the "+C" and "-C", which is what appears to be confusing you.
Unfortunately, the example in this problem is a very bad one for trying to clear that confusion, because a phase shift of EITHER pi/3 or -pi/3 produces the SAME graph, so using the "+C" or "-C" form both give correct answers.
In my experience, the form that is virtually always used is the one with "-C". That makes it consistent with the discussion of other types of (non-cyclic) graphs, such as a parabola, where  is always used to represent a shift h units to the right.
So I myself would object to being asked to write the equation of the function shown in the graph in the form
y = A sin B(x + C) + D
But, as I pointed out a bit earlier, with this particular graph it doesn't matter which form you use, because, with either form, C can be either pi/3 or -pi/3.
So given all that, I would use the form
y = A sin B(x-C) + D
and analyze the given graph as follows.
The maximum and minimum values are 1 and -3, so the midline is -1 and the amplitude is 2. That gives us D=-1 and A=2.
The period is 2pi/3. B is (2pi) divided by the period, so B=3.
For the parent sine graph, the function is at the midline and is increasing at 0. In this example, that happens at both pi/3 and -pi/3. So for this graph I can use either C=pi/3 or C=-pi/3.
That gives me answers that are those shown in your answer key:
y = 2 sin 3(x-pi/3) + (-1)
Finally, it should be pointed out that, although "amplitude" is always positive, in the equation A can be negative.
For the basic sine graph with A negative, the function is at the midline and is decreasing at 0, which is the case with this graph. So a different correct equation for the given graph would have A=-2 with 0 phase shift, so C would be 0.
That would give us different correct answer to the problem:
A=-2; B=3; C=0; D=-1
y = -2 sin 3(x) + (-1)
|
|
|
