subtract 5 from both sides of the equation to get:
cot(x) = 1
since cot(x) = 1/tan(x), you get:
1/tan(x) = 1
solve for tan(x) to get:
tan(x) = 1/1 = 1
if your calculator is set to degrees....
solve for x to get:
arctan(1) = 45 degrees.
tangent is positive in the first and third quadrants.
the equivalent angle in the third quadrant is 180 + 45 = 225 degrees.
in the interval between 0 and 360 degrees, your angle will be 45 degrees and 225 degrees.
here's what it looks like on a graph.

if your calculator is set to radians....
solve for x to get:
arctan(1) = .7853981634 radians.
tangent is positive in the first and third quadrants.
the equivalent angle in the third wuadrant is pi + .7853981634 = 3.926990817 radians.
in the interval between 0 and 2pi radians, your angle will be .7853981634 radians and 3.926990817 radians.
here's what it looks like on a graph.
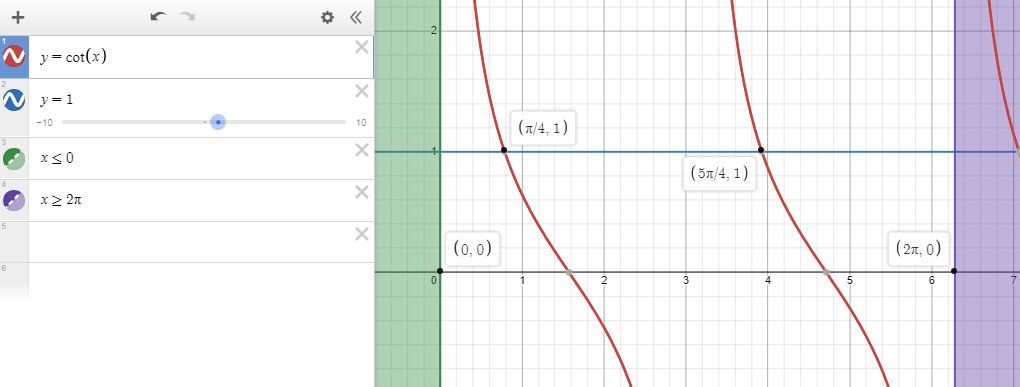
note that .7853981634 radians is equal to .25 * pi radians which is equal to pi/4 radians, as shown on the graph.
note also that 3.926990817 radians is equal to 1.25 * pi radians which is equal to 5pi/4 radians, as shown on the graph.
note that most calculators don't handle cotangent function directly.
my ti-84 plus is one of them.
to solve for cotangent, it is necessary to convert cotangent to equivalent tangent function.
as an example:
if cotan(x) = 7, then 1/tan(x) = 7.
solve for tan(x) to get tan(x) = 1/7.
calculator says that x = arctan(1/7) = 8.130102354 degrees.
that should be your angle.
cot(8.120102354) should be equal to 7.
since cot = 1/tan, then 1/tan(8.120102354) = 7
use your calculator to get 1/tan(8.120102354) = 7.
the graphing software i use (desmos.com) can handle cotangent function directly, as you can see.