SOLUTION: A plane flies on a true bearing of 320° for 450 km. It then flies on a true bearing of 350° for 130 km and finally on a true bearing of 050° for 330 km. How far north of its sta

Question 1203473: A plane flies on a true bearing of 320° for 450 km. It then flies on a true bearing of 350° for 130 km and finally on a true bearing of 050° for 330 km. How far north of its starting point is the plane?

Found 3 solutions by Theo, ikleyn, math_tutor2020:
Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
solutions are in the displays shown abelow:

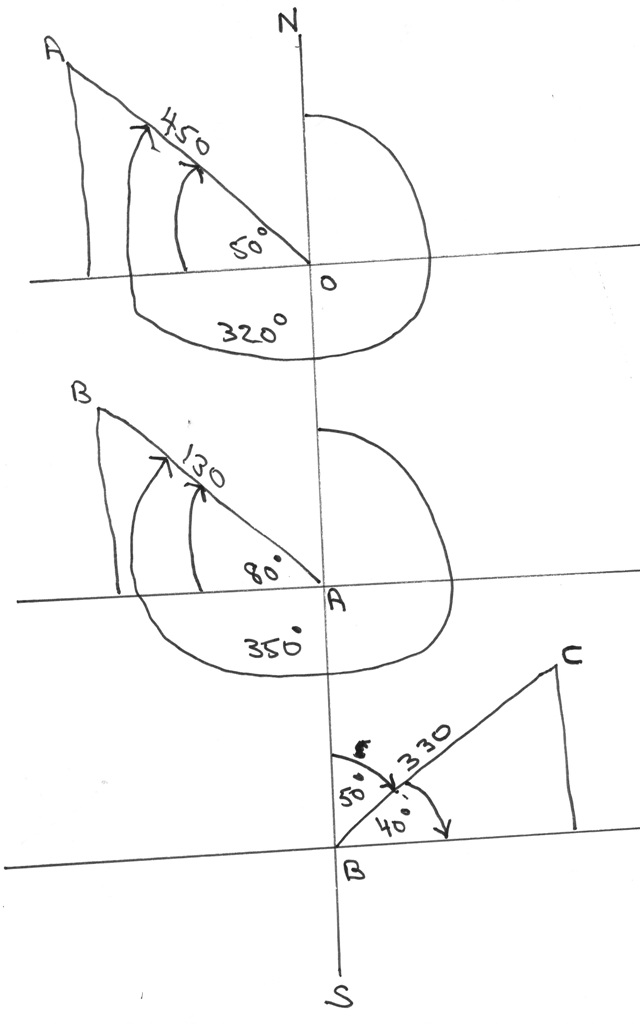
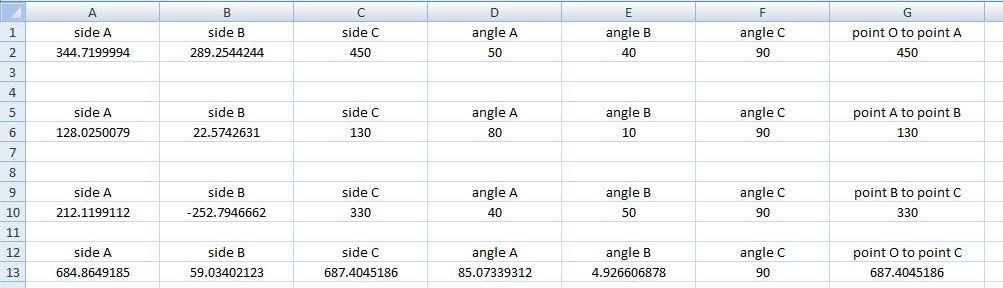
first disp;lay shows calulations for acute angles of the triangles formed for point 0 to point A, then point A to point B, then point B to point C.

320 is equal to 270 + 50.
350 is equal to 270 + 80.
50 is equal to 90 - 40.

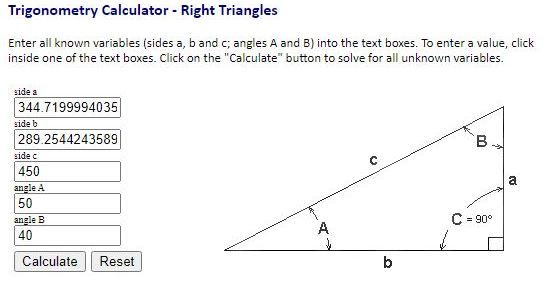
calculator is used to find the horizontal and vetical lengths of the triangle.

first one is for point 0 to point A,

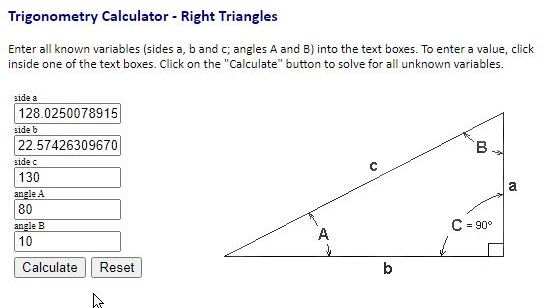
second one is for point A to point B.

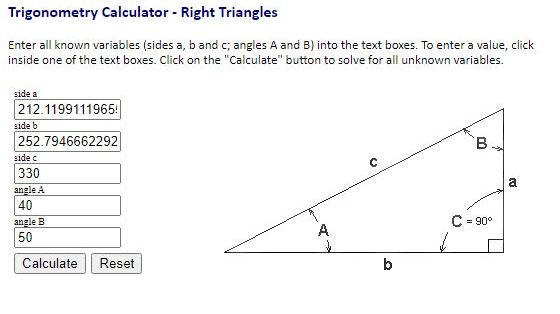
third one is for point B to point C.

excel was used to find lengths of the vertical and horizontal legs of the triangles formed, as shown below:

sketch below shows the total layout and hot it would appear with all locations together on the same sheet in their approximate locations relative to each other.

this also shows the final calculation from pont O to the final point C.

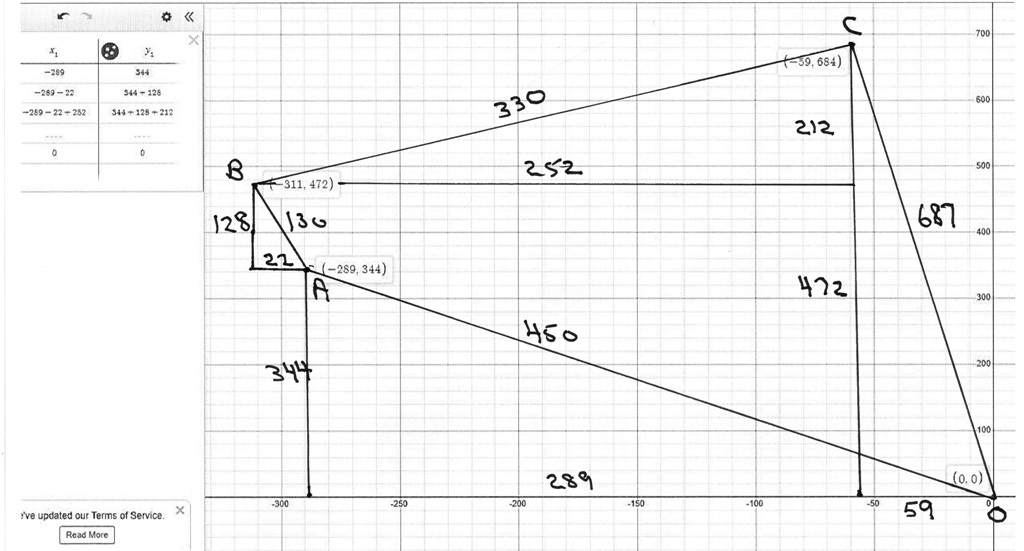
you were asked to find the total distance going north.

that would be the sum of the vertical distances from point 0 to point A, point A to point B, and point B to point C.

that would be 684.86 as shown in the spreadsheet column A row 13.

that would also be 212 + 472 = 684 as showon in the final sketch.

the procedure used was to find the triangles involved and then calculate the vertical and hosizontal lets of those triangles.

in the final diagram, the 472 vertical length shown is the sum of 344 and 128.

here's a reference on bearings.

https://www.mathsteacher.com.au/year7/ch08_angles/07_bear/bearing.htm

let me know if you have any questions.

theo

Answer by ikleyn(52776)   (Show Source): You can put this solution on YOUR website!
.
A plane flies on a true bearing of 320° for 450 km.
It then flies on a true bearing of 350° for 130 km
and finally on a true bearing of 050° for 330 km.
How far north of its starting point is the plane?
~~~~~~~~~~~~~~~~~~

        While solving this problem, I will assume that the Earth surface is flat :)

In this problem, all angles are counted from the Northern direction (from y-axis) clockwise. The question asks "how far North is the plane from its starting point?" To answer this question, it is enough to add algebraically all projections of partial displacements on y-axis. This formula does it how far North = 450*cos(320°) + 130*cos(350°) + 330*cos(50°) = = 450*0.7660444 + 130*0.9848077 + 330*0.642787 = 684.864691 kilometers. +---------------------------------------------------------+ | I use cosine function, since in this problem | | it provides projections of displacements on y-axis. | +---------------------------------------------------------+ ANSWER. 684.86 kilometers, rounded.

Solved (in a way as it is expected and as it SHOULD be done).

====================

By the way, for your better understanding, the precision in this problem
should not be smaller than the size of the plane (which is tens of meters),
otherwise the answer is illogical and makes no sense

When the other tutor, while retelling my solution, reproaches me for inaccuracy in one unit
in the last 6th decimal place (which corresponds to one millimeter) in the intermediate calculation,
(before I made my final rounding), it is just out of common sense.

\\\\\\\\\\\\\\\\\\

The formula, which I use, is a standard formula from adding vectors on a coordinate plane.
This formula is a prerequisite for solving such problems. So, at normal teaching process,
you should learn this formula before you get this problem as an assignment.
It is why I do not repeat what you should know from your teacher/professor or from your textbook.

Answer by math_tutor2020(3816)   (Show Source): You can put this solution on YOUR website!

The answer is approximately 684.864918 km. I rounded to 6 decimal places. Feel free to round however else your teacher instructs. I have confirmed this answer with GeoGebra.

Tutor ikleyn has a value (684.864691) close to what I got. However there's slight rounding error. The "684.864" portions match up at least.

Tutor theo has at least one error in his calculations. The good news is that 687.4045186 is somewhat close to 684.864918

I'll explain why the formula ikleyn uses works.

The four key bearing angles to memorize are:
000° = north
090° = east
180° = south
270° = west
Check out the diagram below.
Basically we start aiming north. Then rotating clockwise will increase the bearing angle.

So let's say the bearing is 050° and we move 100 km along this bearing.
We move 100 km along the red arrow.

We want to know how far north we are from the origin.
Thus we want to find the vertical leg of this right triangle marked in red.
cos(angle) = adjacent/hypotenuse
cos(50) = adjacent/100
adjacent = 100*cos(50)

Therefore the north-south displacement for this example is 100*cos(50) = 64.27876 km approximately.

In general if you move r units along bearing theta degrees, then r*cos(theta) units is the north-south displacement.
Negative displacement means we move south, while positive displacements move us north.

This idea can then be applied many times to chain together multiple movements.
That is how ikleyn ended up with the formula: 450*cos(320°) + 130*cos(350°) + 330*cos(50°)
Make sure your calculator is in degree mode. A quick check could be something like cos(60°) = 0.5 which you should have memorized.

Feel free to ask any further questions if you're still stuck.

RELATED QUESTIONS
A plane flies 760 km due north then flies on a bearing of 220� until it is due west of... (answered by josgarithmetic)
An airplane flies 200 km on a bearing of 335°. It then flies 100 km on a bearing of... (answered by Alan3354)
An aircraft flies from A to C on a bearing of 27degree. It then changes course and flies... (answered by Theo)
A helicopter flies 30 km from a point P to another point Q on a bearing of 128°. It then (answered by Alan3354)
A plane flies 285 km due west and then 320 km due north. what are its distance and... (answered by fractalier)
a plane flies 285 km due west and then 320 km due north. What are its distance and... (answered by psbhowmick)
A plane flies on a bearing of 230o at 350 miles per hour. A wind is blowing from the... (answered by Alan3354)
A pilot takes off from Amber Island and flies for 150 km at 040T to BarterIsland where... (answered by Theo)
A plane flies 500 kilometers with a bearing of N 44 degrees W from B to C. The plane then (answered by Fombitz)