Question 1203377: Draw an angle in standard position with the given measure. -120 degrees
Found 4 solutions by Edwin McCravy, math_tutor2020, Theo, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website!
Positive angles rotate counter-clockwise from the right side of the x-axis.
Negative angles rotate clockwise from the right side of the x-axis.
This is a negative angle, so it rotates clockwise through 120o from the right
side of the x-axis.
Edwin
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Add on 360 degrees to do a full rotation
-120+360 = 240
The angles -120 degrees and 240 degrees are coterminal angles.
They both point in the same exact direction.
We'll have 0 degrees pointing directly east (aka to the right).
Then rotate counter-clockwise so that 90 degrees points north, 180 degrees points west, and 270 degrees points south.
The angle 240 degrees is in quadrant III, the southwest quadrant.
Notice that rotating 240 degrees counter-clockwise (in red) is the same as rotating 120 degrees clockwise (in blue)
Edit:
When looking at a clock face, there are 4 spaces when rotating from 3 to 4 to 5 to 6 then to 7.
Each gap is 30 degrees (because 360/12 = 30), which means 4 gaps give 4*30 = 120 degrees total.
Therefore, rotating clockwise from 3 o clock (east) to 7 o clock is a 120 degree rotation.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! here is a picture of your angle in the standard position.
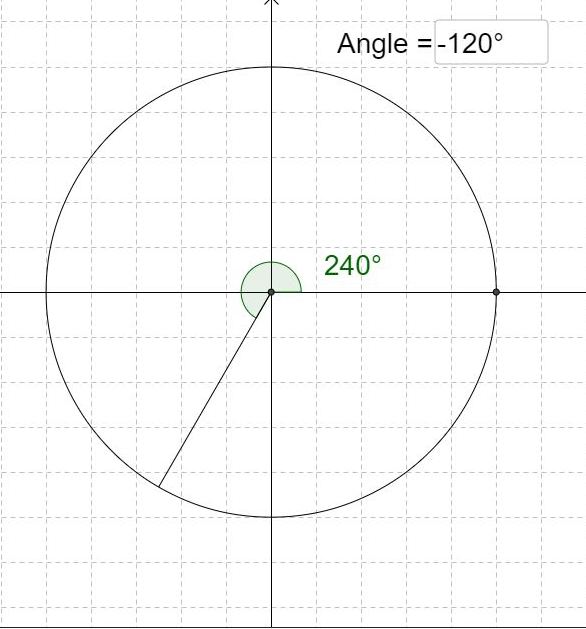
this angle was created using the software at https://www.geogebra.org/m/qBfHYSTQ
you put the angle in the box indicated and the software generates the graph.
one thing you need to now.
the software shows you the equivalent positive angle, not the negative angle.
the equivaalent positive angle is obtained by additing 360 to the negative angle until it becomes positive and between 0 and 360 degrees.
-120 + 360 = 240.
the positive angle in the same position as the negative angle of -120 degrfees is equal to 240 degrees.
when graphing either of those angles, the graph wlll show the angle in the same position.
if you look at the graph of -120 degrees and you look at the graph of 240 degrees, the graphs will be identical.
you can see that for youself by executing the software and entering -120 first and then 240 next.
the graphs will be identical.
Answer by ikleyn(52781)  (Show Source):
|
|
|
