SOLUTION: sin [arccos(-square root 7)/5] answers can be: 4 square root 2/5 -4 square root 2/5 3 square root 2/5 -3 square root 2/5 I a

Algebra.Com
Question 1201902: sin [arccos(-square root 7)/5]
answers can be: 4 square root 2/5
-4 square root 2/5
3 square root 2/5
-3 square root 2/5
I am lost as to how to solve
Found 5 solutions by Edwin McCravy, greenestamps, ikleyn, Theo, Alan3354:
Answer by Edwin McCravy(20054)   (Show Source): You can put this solution on YOUR website!


We first look only at 

This asks for the "arc"-angle whose cosine is 

When you see "arc" in front of a trig function, it always means you want
an angle that has what's in the parentheses for that trig function.

If it had asked for any "arc"-angle of a POSITIVE number, the answer would
always be taken in the first quadrant between 0 and π/2.

However, it is asking for the arccosine of a NEGATIVE number.  Learn these:

arcsin of a negative is an angle between -π/2 and 0 in QIV
arccos of a negative is an angle between  π/2 and π in QII
arctan of a negative is an angle between -π/2 and 0 in QIV

So we know that  is an "arc" angle in QII.
We draw a right triangle in QII which has a cosine of .
The red arc drawn counterclockwise for the right side of the x-axis,
represents the "arc" angle.  Since the cosine of the arc angle is 
, and since , we put
the numerator  on the adjacent side, and the denominator, 5,
on the hypotenuse. (Notice that we took the adjacent side to be NEGATIVE
because it goes LEFT. The hypotenuse is ALWAYS POSITIVE.)



Then we use the Pythagorean theorem to find the opposite side.








The opposite side goes upward so we take the + sign.




Now finally we go back to the beginning



It is the sine of that arc angle that we want. We know that 
, so



Edwin
Answer by greenestamps(13198)   (Show Source): You can put this solution on YOUR website!


The expression to be evaluated is "the sine of the angle whose cosine is (-square root of 7)/5".

Use to find the answer.




or

We need to determine which of those answers is correct (they are both answer choices).

To do that, we need to know something about the arc cosine function.

The interval closest to 0 on which the cosine function takes on all its values is from 0 to pi; i.e., the angle is either in quadrant I or quadrant II. Cosine is positive in quadrant I and negative in quadrant II. Since the cosine of the angle in this problem is negative, the angle is in quadrant II. And in quadrant II, sine is positive; so the answer is .

ANSWER:
Note that we didn't need to determine that the angle is in quadrant II, because sine is positive in both quadrants I and II.

Note further that, because arccos(x) is always an angle between 0 and pi, and because sin(x) is always positive (or 0) between 0 and pi, this means sin(arccos(x)) is always positive (or 0).
Answer by ikleyn(52765)   (Show Source): You can put this solution on YOUR website!
.

        Instead of this  UNPROFESSIONAL  writing in the post,
        I will write a message in a form as it  SHOULD  BE  presented. 

Find  .

      possible answers list: 

          (a)  

          (b)  

          (c)  

          (d)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


First step is to write professionally.  Withoiut it,  the gate in paradise is closed.
Now,  when it is written professionally,  we can start thinking. 


 is an angle  ,  0 <=  <  such that   = .

Since the cosine is negative, it just tells you that the angle  is in second quadrant, QII.


So, you are given the angle    in QII  such that   = .


And they want you find .  Simple as an orange.  Or a cucumber.


We have   =  =  =  =  = 

                 =  =  = .    ANSWER


Notice that for the sine function, I use the "+" sign before the square root,
since sine is positive in QII.


Your answer is option (c) of the given answer list.

Solved with complete explanations.

------------------

There are two secrets in solution. 

    Secret 1: The problem should be written professionally.


    Secret 2: From the problem, you should clearly understand, what is given 
              and what they want from you, and clearly explain it to yourself.


    After that, the solution will be easy.


I know that for beginner students,  such problems are difficult and perplex them.
The only way to crawl into this area is to get it from an expert and read and re-read it as many times,
as it is needed for full understanding.   There is  NO  OTHER  WAY.


/////////////////


If you want to see other similar and different solved problems,  look into the lesson
    - Advanced problems on calculating trigonometric functions of angles
in this site.


\\\\\\\\\\\\\\\\\\\\\\\


The solution by  @Theo,  giving two possible answers,  is  INCOPRRECT.



Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
first of all, you don't have parentheses where they belong.
that makes it difficult to see what the values really are.
i rewrote the values using parentheses to make it clearer.

after rewriting, i get the expression to be solved is:
sin(arccos(-sqrt(7)/5)
and i get the possible solutions are:
4 * sqrt(2) / 5
-4 * sqrt(2) / 5
3 * sqrt(2) / 5
-3 * sqrt(2) / 5

let A be the angle.
arccos(-sqrt(7)/5) means that cos(A) = (-sqrt(7)/5).
since cosine is equal to adjacent side divided by hypotenuse, you get:
adjacent side is -sqrt(7) and hppotenuse is 5.
the adjacent side is the x value on the graph.
the opposite side is the y value on the graph.
you know that the adjacent side is negative, so the angle will be either in the second quadrant or the third quadrant.
the hypotenuse is always positive.
you can use pythaorus to find the value of the opposite side.
pythgorus says tha adjacent side squared plus opposite side squared = hypotenuse squared.
you get:
x^2 + y^2 = h^2.
x represents the adjacent side.
y represens the opposite side.
h represents the hypotenuse of thetriangle formed.
A represents the angle.
since you know the value of x and the value of h, the formula becomes:
(-sqrt(7))^2 + y^2 = 5^2
simplify to get:
7 + y^2 = 25
solve for y^2 to get y^2 = 18
solve for y to get y = plus or minus sqrt(18).
if y is positive, then the angle is in the second quadrant.
if y is negative, then the angle is in the third quadrant
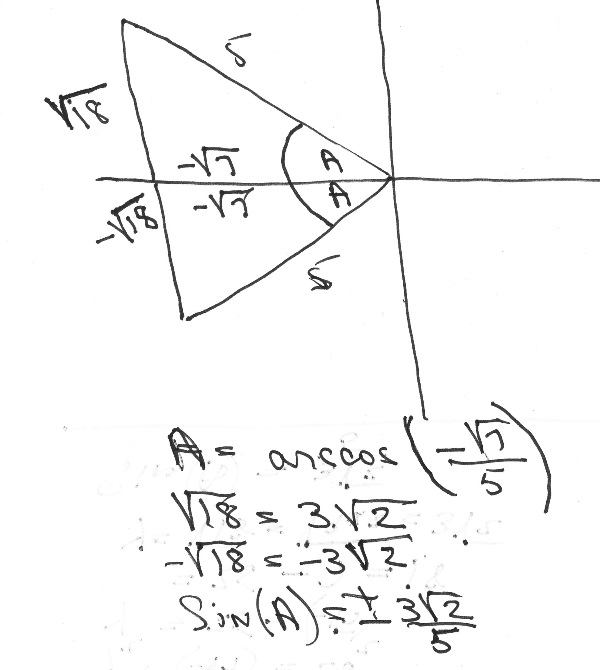
here'smy diagram of how i see the graphical representation.
note that angle A in the diagram is the reference angle.
in this problem, you really don't need to solve for the reference angle.
the problem can be solvedby the other values you are given.

A is your reference angle.
in the second quadrant, your angle would be 180 minus A.
in the third quadrant, your angle would be 180 plus A.

your original expression was sin(arccos(-sqrt(7)/5)
we said that arccos(-sqrt(7)/5) means that cos(A) = -sqrt(7)/5.
from that information, and from drawing the diagram, we were able to find that the adjacent side of angle A was -sqrt(7) and the hypotenuse was 5.
from that information, we were able to determine that the opposite side was either sqrt(18) or - sqrt(18).
if the angle was in the second quadrant, then opposite side was sqrt(18).
if the angle was in the third quadrant, then opposite side ws -sqrt(18).

if we simplify sqrt(18), we find that sqrt(18) = 3 * sqrt(2).
therefore sin(A) was equal to 3 * sqrt(2) if the angle was in the second quadrant and sn(A) was equal to -3 * sqrt(2) if the angle was in the third quadrant.

i beieve your solution is that sin(arccos(-sqrt(7)/5)) is either 3 * sqrt(2) / 5 or -3 * sqrt(2) / 5.

here's my sketch.



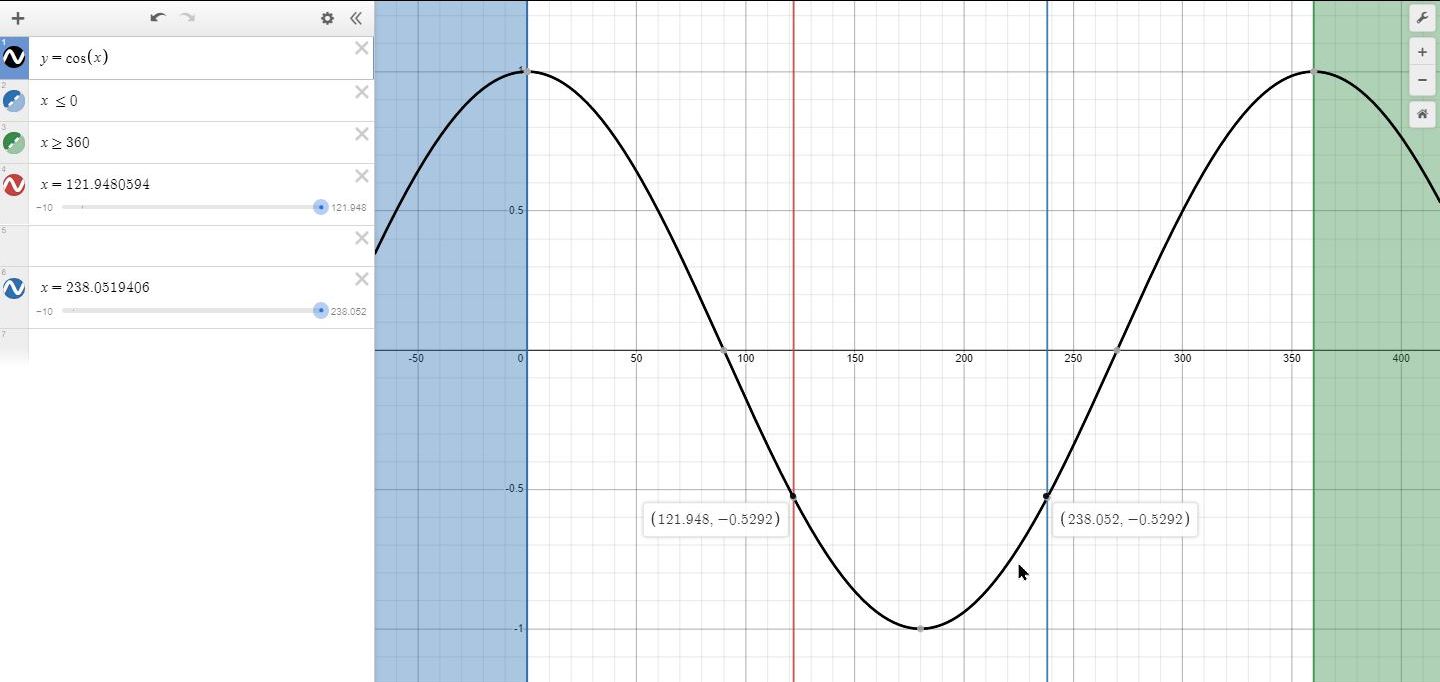
here's my graph of cos(x) which shows the angles in the second quadrant (121... degrees) and the third quadrant (238... degrees) have the same cosine value.



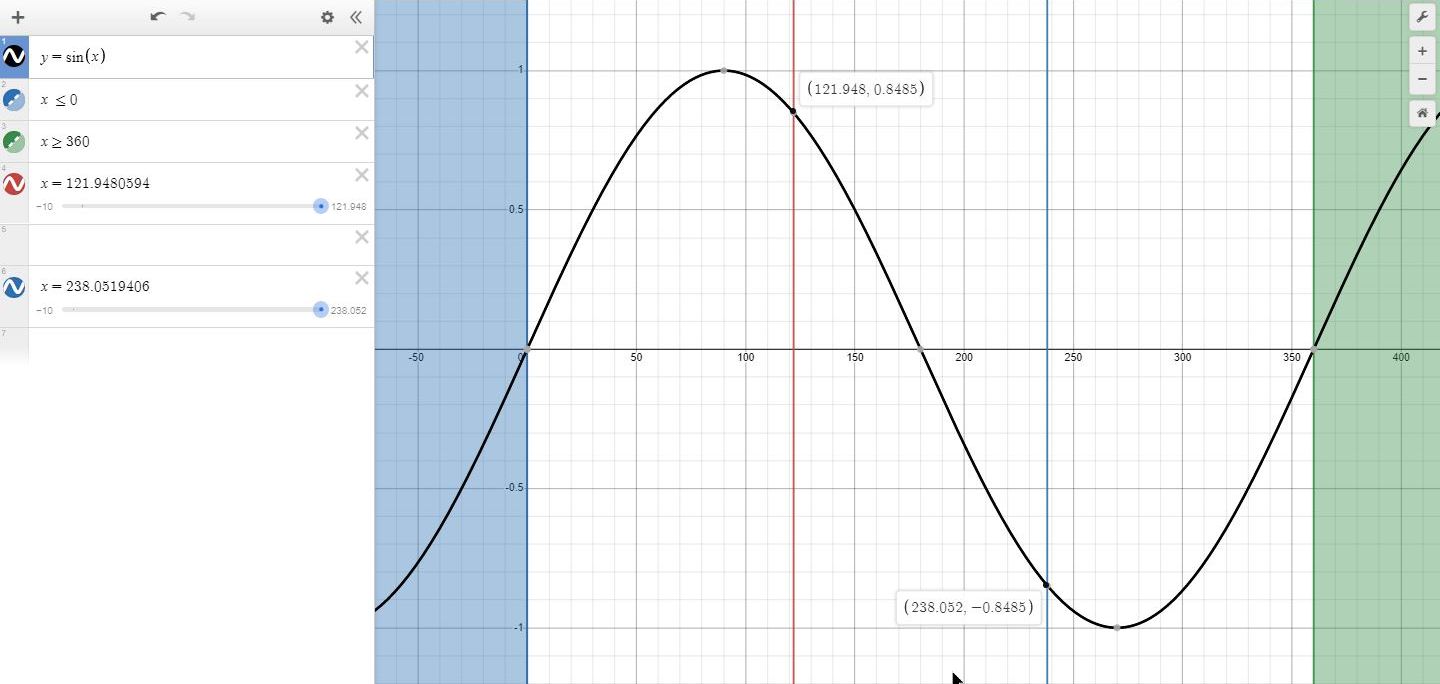
here's my graph of sin(x) which shows the angles in the second quadrant (121... degrees) and the third wuadrant (238... degrees) have the same sine value, but with different signs (positive in the second quadrant and negative in the third quadrant).



if all this seems confusing, don't feel bad, because it is confusing and very difficult to figure out unless you've had experience in working out problems such as these.

i'm reasonably confident the answers i gave you are correct.
let me know if you have any questions.
theo
Answer by Alan3354(69443)   (Show Source): You can put this solution on YOUR website!
sin [arccos(-square root 7)/5]
---------
cos [arccos(-square root 7)/5] = -sqrt(7)/5
-------------
sin = sqrt(1 - cos^2) = sqrt(1 - 7/25) = sqrt(18/25)
=
RELATED QUESTIONS

square root 2 - 5 square root 3 + 7 square root 2 + 9 square root... (answered by Mathtut)
numerator :2 square root 3 - square root 5 denominator:2 square root 2 + square root... (answered by math-vortex)
5 + square root 3 over 7-2 square root... (answered by stanbon,solver91311)
Square root 5 (square root 5 - square root 2) + square root 2 (square root... (answered by mananth)
(3 square root... (answered by Mathtut)
3/ 5- square root... (answered by stanbon)
(3+square root of 5)squared=(3+square root 5)(3+square root 5) (answered by tns_tutor5000)
4over square root 5 +square root 3 I worked it to 4(square root 5 -square root 3) over 2 (answered by jim_thompson5910)
2 square root of 5 --------------------- -4 + square root of... (answered by solver91311)