Find the 3 cube roots of -8 in polar form.
-8 = -8+0i
Graph the vector whose magnitude (modulus) is r=8, whose tail is at (0,0),
and whose tip is at (-8,0), and whose argument (angle) is θ=180o.
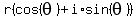
Since the cube root is the 1/3 power:
We raise everything to the 1/3 power. In doing so we will use deMoivre's
theorem, where we raise the magnitude (modulus 8) to the 1/3 power (i.e.,
take its cube root 2), and multiply its argument (angle) by 1/3.
Now, since there are 3 cube roots, we take three consecutive integers for n.
Let n=0
Let n=1
Let n=2
.
[Notice that the second one would turn out to be 2(-1+0i) or just -2, which
is the real cube root of -8.]
Edwin
