Question 1162249: Find the exact values of sin(2θ), cos(2θ), and tan(2θ) when sin θ =-7/12 and 180∘ < 𝜃 < 270∘.
Found 3 solutions by Theo, Edwin McCravy, MathTherapy:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! here's how i think it's going to work.
you have sin(x) = -7/12
that makes x = -35.68533471.
add 360 to that to get the equivalent positive angle of 324.3146653.
the reference angle for that is 360 - that = 35.68533471.
the equivalent angle for that in the third quadrant is that plus 180 = 215.6853347.
take the sine of that and you get -7/12, which is the correct sine for angle x in the third quadrant.
you should be able to simply find sin(2x), cos(2x), tan(2x), by simply doubling that angle.
2 times 215.6853347 = 431.3706694.
you have:
x = 215.6853347
2x = 431.3706694
sin(2x) = .9476050057
cos(2x) = .3194444444.....
tan(2x) = 2.9664567.
if my assumptions are correct, those are your solutions.
using trigonometric identities, you shouls get the same answers.
you are given that sin(x) = -7/12
that makes x = 215.6853347, as we found out earlier.
the trigonometric identifies are:
sin(2x) = 2 * sin(x) * cos(x)
cos(2x) = cos^2(x) - sin^2(x)
tan(2x) = 2 * tan(x) / (1 - tan^2(x)
since we know x, we should be able to find those using the trig identities.
sin(x) = -.5833333333 stored in variable N
cos(x) = -,8133248621 stored in variable O
tan(x) = .7181848465 stored in variable P
i stored the values in those variables so i don't have to rewrite those values each time i use them.
the trigonometric identifies are rewritten using those variable names as shown below:
sin(2x) = 2 * N * O = .9476050057
cos(2x) = O^2 - N^2 = .3194444444
tan(2x) = 2 * P / (1 - P^2) = 2.96641567.
i get the same answers, so both methods seem to work.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by MathTherapy(10556)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the exact values of sin(2θ), cos(2θ), and tan(2θ) when sin θ =-7/12 and 180∘ < 𝜃 < 270∘.
The other person who responded gave you WRONG answers. The problem asks for EXACT VALUES. What he gave you are NOT exact values!
 . We then need to find A, or x, which will be negative, since . We then need to find A, or x, which will be negative, since  is an ∠ in the 3rd quadrant (180∘ < 𝜃 < 270∘). is an ∠ in the 3rd quadrant (180∘ < 𝜃 < 270∘).

Therefore, THREE of the 6 TRIG. RATIOS are: 
You may not need tan 𝜃, depending on which formula you use.
For me, since I would've determined sin 2𝜃 and cos 2𝜃, I would then use the formula:  . Then again, you decide!! . Then again, you decide!!
Below, I've done  for you. Follow that same concept to determine cos 2𝜃 and maybe tan 2𝜃. for you. Follow that same concept to determine cos 2𝜃 and maybe tan 2𝜃.

 ------ Substituting ------ Substituting 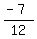 , for, sin 𝜃, and , for, sin 𝜃, and 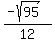 for cos 𝜃. for cos 𝜃.

BTW, Edwin, your tan 𝜃 is WRONG!!
|
|
|