secant is equal to 1/cos and tangent is equal to sin/cos, therefore:
the equation becomes 1/cos^2(a) + 5 = 3*sin^2(a)/cos^2(a).
multiply both sides of this equation by cos^2(a) to get:
1 + 5*cos^2(a) = 3*sin^2(a)
sin^2(a) is equal to 1 = cos^2(a).
the equation becomes:
1 + 5*cos^2(a) = 3*(1 - cos^2(a))
simplify to get:
1 + 5*cos^2(a) = 3 - 3*cos^2(a)
subtract 1 from both sides of the equation and add 3*cos^2(a) to both sides of the equation and combine like terms to get:
8*cos^2(a) = 2
solve for cos^2(a) to get:
cos^2(a) = 2/8 = 1/4
solve for cos(a) to get:
cos(a) = plus or minus 1/2.
solve for a to get:
a = plus or minus arccos(1/2)
in degrees, a would be equal to 60 degrees for arccos(1/2) or 120 degrees for -arccos(1/2).
60 degrees * pi / 180 = pi/3 in radians.
120 degrees * pi / 180 = 2pi/3 in radians.
those would be your answers after they're confirmed.
to confirm, replace a with those answers after your set your calculator to radians and evaluate the original equation to see if it's true.
the original equation is:
sec^(a) + 5 = 3 * tan^2(a)]
when a = pi/3 radians, that becomes:
sec^2(pi/3) + 5 = 3 * tan^2(pi/3)
if your calculator doesn't do secant directly, than substitute 1/cos^2(pi/3) for sec^2(pi/3).
you will get:
9 = 9, confirming pi/3 is one of the angles.
when a = 2pi/3 radians, that (the original equation) becomes:
1/cos^2(2pi/3) + 5 = 3 * tan^2(2pi/3)
you will get:
9 = 9, confirming 2pi/3 is also one of the angles.
note that a can also be 360 - 60 = 300 degrees * pi/180 = 5pi/3 and a can also be 180 + 60 = 240 * pi / 180 = 4pi/3.
you can graph the original equations to see if they're equal at those angles.
the graph confirms that sec^2(a) + 5 is equal to 3 * tan^2(a) for a = pi/3, 2pi/3, 4pi/3, 5pi/3 in the interval of a = 0 to 2pi.
the graph looks like this:
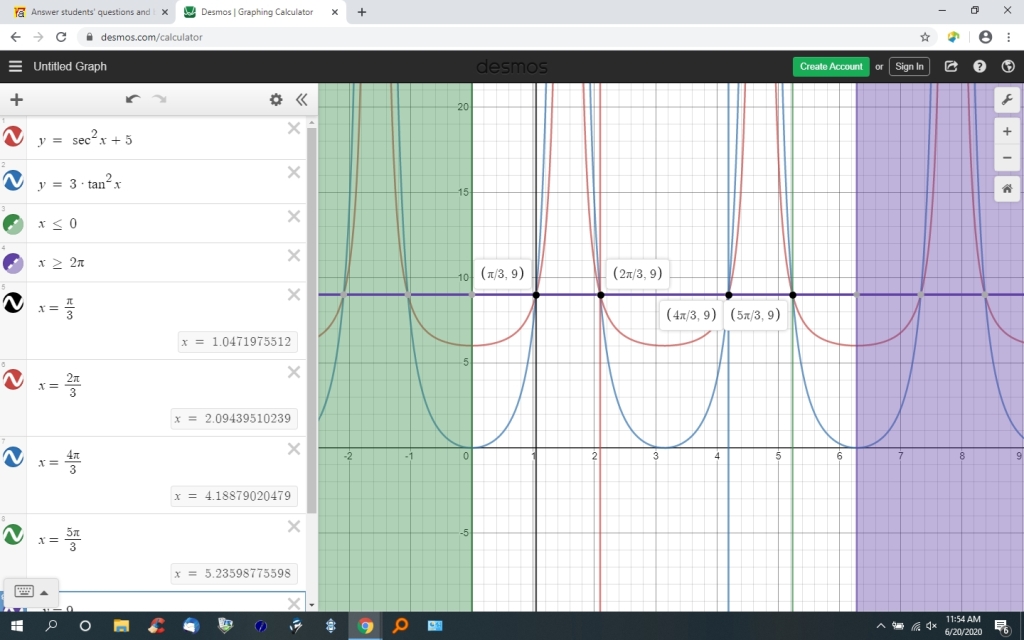
since you are not restricted to the interval from a = 0 to a = 2pi, then there are an infinite number of angles that will satisfy the equation.
those angles would be:
pi/3 plus or minus k * 2pi
2pi/3 plus or minus k * 2pi
4pi/3 plus or minus k * 2pi
5pi/3 plus or minus k * 2pi
all of those angles satisfy the equation.
k is an integer greater than or equal to 0.
as one example, take a = 5pi/3 and let k = plus or minus 5
when k = 0, the angle is 5pi/3 which we already know satisfies the equation because 1/cos^2(5pi/3) + 5 = 9 and 3 * tan^2(5pi/3) = 9
when k = -5, 5pi/3 becomes 5pi/3 - 5 * 2pi which becomes 5pi/3 - 10pi which becomes 5pi/3 - 30pi/3 which becomes -25pi/3.
1/cos^2(-25pi/3) + 5= 9
3 * tan^2(-25pi/3) = 9
that angle satisfies the equation.
when k = 5, 5pi/3 becomes 5pi/3 + 5 * 2pi = 5pi/3 + 10pi which becomes 5pi/3 + 30pi/3 which becomes 35pi/3.
1/cos^(35pi/3) + 5 = 9
3 * tan^2(35pi/3) = 9
that angle also satisfies the equation.
on a graph, that looks like this:
