Question 1156326: Outside temperature over a day can be modeled as a sinusoidal function. Suppose you know the temperature varies between 66 and 104 degrees during the day and the average daily temperature first occurs at 9 AM. How many hours after midnight, to two decimal places, does the temperature first reach 76 degrees?
Answer by greenestamps(13208)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are many ways to set this problem up for solving. Here's how I would do it.
The average temperature is first reached at 9am. At that time the temperature is increasing. Average temperature and temperature increasing means we can use a basic sine function with "zero" being at 9am.
With 66 and 104 for the minimum and maximum temperatures, the center line is 85 and the amplitude is 19.
Instead of trying to figure out a period for the function in terms of hours, simply let a period be 360 degrees.
Then an equation for the function is
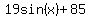 [x in degrees] [x in degrees]
Here is a graph (window [-30,360,-10,120]) of the function and the constant 76:

We want to find how many hours after midnight it is when the temperature first reaches 76 degrees. On the graph, that is near the right edge where the temperature function and the constant function intersect.
A graphing calculator shows the intersection at (331.72629,76)
According to the way I have decided to graph the function, that means a temperature of 76 degrees is first reached 331.72629/360 of a day after 9am. Convert that to hours and add it to 9am.

9am plus 22.1151 hours is 31.1151 hours, or 7.1151 hours after midnight.
Rounding to 2 decimal places....
ANSWER: The average temperature is first reached 7.12 hours after midnight.
Since there are many different ways to set this problem up, I hope you get responses from other tutors showing different methods which may or may not be more to your liking....
|
|
|