Question 1151227: if an equilateral triangle has area equal to 10, what is its height?
A) 5 / sqrt(3)
B) sqrt(10) * (root(4)(3))
c) sqrt(40) / (root(4)(3))
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
h = height of equilateral triangle
x = side length of equilateral triangle
Start with equilateral triangle ABC. Mark point D as the midpoint of one of the sides and draw a line to the opposing vertex. In this case, I marked the midpoint of AB and connected that to vertex C. This forms the height of the triangle. CD is perpendicular to AB. The base here is AB = x, half of which is x/2.

Focus on triangle CDB
a = x/2 and b = h are the two legs
c = x is the hypotenuse
Use the Pythagorean Theorem to solve for h
a^2 + b^2 = c^2
(x/2)^2 + h^2 = x^2
(x^2)/4 + h^2 = x^2
h^2 = x^2 - (x^2)/4
h^2 = (4x^2)/4 - (x^2)/4
h^2 = (4x^2-x^2)/4
h^2 = (3x^2)/4
h = sqrt( (3x^2)/4 )
h = sqrt(3x^2)/sqrt(4)
h = (sqrt(x^2)*sqrt(3))/sqrt(4)
h = (x*sqrt(3))/2
h = (x/2)*sqrt(3)
Plug this into the area of a triangle formula to get the area of an equilateral triangle formula
A = (1/2)*b*h
A = (1/2)*x*(x/2)*sqrt(3)
A = (1/4)*x^2*sqrt(3)
Now plug in the given area A = 10 and solve for x.
10 = (1/4)*x^2*sqrt(3)
10*4 = x^2*sqrt(3)
40 = x^2*sqrt(3)
x^2*sqrt(3) = 40
x^2 = 40/sqrt(3)
x = sqrt(40/sqrt(3))
x = sqrt(40)/sqrt(sqrt(3))
x = sqrt(40)/(3^(1/4))
x = sqrt(40)/root(4,3)
x = sqrt(4*10)/root(4,3)
x = sqrt(4)*sqrt(10)/root(4,3)
x = 2*sqrt(10)/root(4,3)
Now use this to find h
h = (x/2)*sqrt(3)
h = (1/2)*sqrt(3)*x
h = (1/2)*sqrt(3)*( 2*sqrt(10)/root(4,3) )
h = sqrt(3)*sqrt(10)/root(4,3)
h = sqrt(10)*sqrt(3)/root(4,3)
h = sqrt(10)*(3^(1/2))/(3^(1/4))
h = sqrt(10)*3^(1/2-1/4)
h = sqrt(10)*3^(1/4)
h = sqrt(10)*root(4,3)
Answer: B) sqrt(10)*root(4,3)
Note: root(4,3) refers to the 4th root of 3. So root(4,3) can be written as 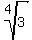 . In terms of exponents, . In terms of exponents, 
------------------------------
Here is an alternate way to get the answer
x = half the side length of the equilateral triangle (eg: DB = x)
h = height of equilateral triangle
a^2 + b^2 = c^2 ... pythagorean theorem
x^2 + h^2 = (2x)^2
x^2 + h^2 = 4x^2
h^2 = 3x^2
h = sqrt(3x^2)
h = x*sqrt(3)
x = h/sqrt(3)
2x = 2h/sqrt(3) is the full base of the equilateral triangle
A = 0.5*base*height
A = 0.5*2x*h
A = 0.5*(2h/sqrt(3))*h
A = h^2*3^(-1/2)
10 = h^2*3^(-1/2)
10*3^(1/2) = h^2
h = (10*3^(1/2))^(1/2)
h = (10)^(1/2)*(3^(1/2))^(1/2)
h = sqrt(10)*(3^(1/2))^(1/2)
h = sqrt(10)*3^(1/4)
h = sqrt(10)*root(4,3)
|
|
|