SOLUTION: The half-life of carbon 14 is 5,730 years. Approximately, how old is a bone that has 70% of its original carbon 14?

Question 1142059: The half-life of carbon 14 is 5,730 years. Approximately, how old is a bone that has 70% of its original carbon 14?
Found 2 solutions by Theo, greenestamps:
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
the formula to use is f = p * e ^ (r * t)

f is the future value
p is the present value
r is the interest rate per time period
t is the number of time periods

if you are looking for the half life, then f = 1/3 and p = 1.

the p becomes silent and the formula becomes 1/2 = e ^ (r * t)

the time is 5730 years.

the formula becomes 1/2 = e ^ (r * 5730)

take the natural log of both sides of the equation to get:

ln(1/2) = ln(e ^ (r * 5730))

since ln(e ^ (r * 5730)) = r * 5730 * ln(e) and, since ln(e) = 1, the formula becomes:

ln(1/2) = r * 5730

divide both sides of this equation by 5730 to get:

ln(1/2) / 5730 = r

solve for r to get:

r = -.000120968094

to confirm this is correct, replace r with that in the original equation to get:

f = e ^ (-.000120968094 * 5730)

solve for f to get:

f = 1/2

that confirms the formula is correct.

the question is...

how old is a bone that has 70% of its original carbon 14?

the formula which was .5 = e^ ( r * t) becomes:

.70 = e ^ (r * t)

when r = -.000120968094, the formula becomes:

.70 = e ^ (-.000120968094 * t)

you take natural log of both sides of this equation and simplify it to get:

ln(.70) = -.000120968094 * t

divide both sides of the equation by -.000120968094 and solve for t to get:

t = ln(.70) /-.000120968094 = 2948.50428 years.

once you find r, you can graph the equation.

it looks like this.

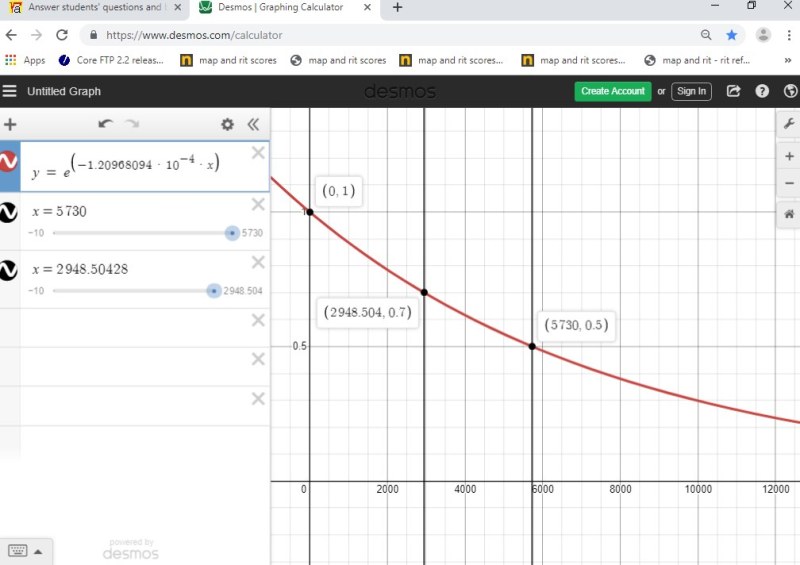
Answer by greenestamps(13200) (Show Source): You can put this solution on YOUR website!

The fraction remaining after n half-lives is .

You want to know when the fraction remaining is 70%, or .7.

The variable is an exponent, so use logarithms:

= 0.514573 to 6 decimal places.

Then the age is the number of half-lives, multiplied by the number of half-lives.

Since the problem says approximately, a good answer is 2950 years.
RELATED QUESTIONS
The half-life of carbon 14 is 5730 years. How old is a bone containing 20% of its... (answered by Fombitz)
The half-life of carbon 14 is 5730 years. How old is a bone containing 20% of its... (answered by Boreal,Theo,josgarithmetic)
If a bome contains 94% of its original carbon-14, how old is the bome? (Carbon-14 has a... (answered by greenestamps)
Hello tutor I really need your help solving this The half-life of carbon 14 is 5730... (answered by josgarithmetic)
Hello Tutors, Can I please have your assistance? The half-life of carbon 14 is 5730... (answered by josgarithmetic)
The half-life of carbon-14 is 5730 years. A bone is discovered which has 30 percent of... (answered by ankor@dixie-net.com)
A skeleton contains one hundredth of its original amount of its original amount of... (answered by stanbon)
an artifact was found and tested for its carbon-14 content. If 87% of the original... (answered by stanbon)
An artifact was found and tested for its carbon-14 content. If 82% of the original... (answered by ankor@dixie-net.com)