it looks like this:
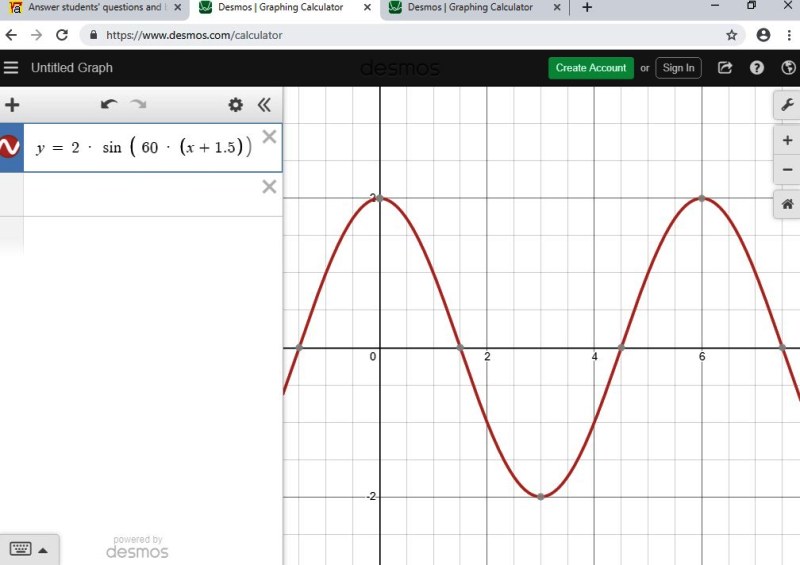
i believe your equation is y = 2 * sin ( pi/3 *(x - 3/2 ) ) when you are working in radians.
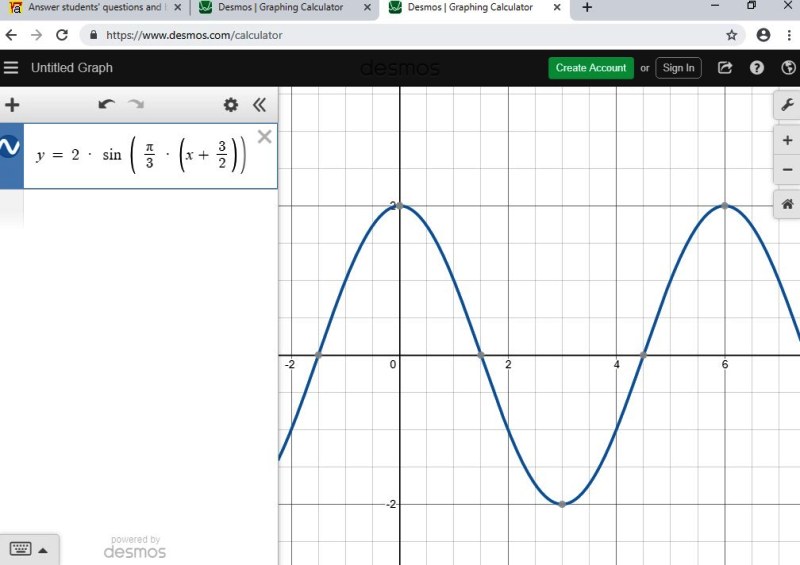
you will notice that both graphs have a period of 6 and that both graphs are identical to each other.
y represents the position of the pistons which represents p for graphing purposes.
x represents time, which represents the variable t for graphing purposes.
in other words, the identical equations are:
p = 2 * sin ( 60 * ( t - 1.5 ) ) when you are working in degrees and .....
p = 2 * sin ( pi/3 *(t - 3/2 ) ) when you are working radians.
the biggest problem i had with this was the horizontal shift.
the first equation i worked was in degrees.
the phase shift to the left was given as pi / 2.
that's in radians.
i converted it to degrees by multiplying it by 180 / pi.
pi / 2 * 180 / pi = 90 degrees.
that, i believe, is the phase shift if the periods was the normal period of 360 degrees.
i then needed to convert that phase shift to when the frequency was 60 rather than 1.
that made the phase shift equal to 90 / 60 = 1.5.
the amplitude was set at 2.
the period was set at 6.
the frequency was 360 / 6 = 60.
that led to the equation you see on the first graph.
when working in radians, ......
the amplitude was still 2.
the period was still 6.
the frequency became 2 * pi / 6 = 2/6 * pi = pi / 3.
the phase shift became (pi / 2) / (pi / 3) which became (pi / 2) * (3 / pi) which became 3 / 2.
that's the same as 2.5, even though i left it at 3 / 2.
that led to the equation you see on the second graph.
i had a hell of a time finding references to phase shift in relationship to frequency, but i think i got a hint from the following reference.
https://www.mathway.com/examples/trigonometry/graphing-trigonometric-functions/amplitude-period-and-phase-shift?id=342
what this is saying is, i think, .....
formula is y = sin ( 60 * x + 90) which is then translated to:
y = sin (60 * (x + 90 / 60) which then becomes y = sin (60 * (x + 1.5)
the shifting rules are:
if the shift is to the left, then it's x + c.
if the shift is to the right, then it's x - c.
this was probably the most confusing part for me and i hope that i got it right.
the degree formula just didn't work when i did it any other way.
this way, both the degree formula and the radian formula give the same answer which is a pretty good clue that it's probably right.