SOLUTION: what are the zeros of f(x) = 4 sin^2 x - 3 on the interval [0, 2pi]?

Algebra ->  Trigonometry-basics -> SOLUTION: what are the zeros of f(x) = 4 sin^2 x - 3 on the interval [0, 2pi]?      Log On


   

Question 1125522: what are the zeros of f(x) = 4 sin^2 x - 3 on the interval [0, 2pi]?
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52754) About Me  (Show Source):
You can put this solution on YOUR website!
.
4 sin^2 x - 3 = 0   is equivalent to


4 sin^2 x = 3       is equivalent to


sin^2(x) = 3/4      is equivalent to


sin(x) = +/- sqrt%283%29%2F2.



Case a).   sin(x) = sqrt%283%29%2F2  has two solutions in the given interval:

           x = pi%2F3   and   x = 2pi%2F3.



Case b).   sin(x) = -sqrt%283%29%2F2  has two solutions in the given interval:

           x = 4pi%2F3   and   x = 5pi%2F3.



Answer.  The zeroes of the function  f(x) = 4 sin^2 x - 3  in the interval [0,2pi)  are

         x = pi%2F3,  x = 2pi%2F3,   x = 4pi%2F3   and   x = 5pi%2F3.

Solved.


Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
let y = f(x).

equation becomes y = 4 * sin^2(x) - 3

set y = 0 and the equation becomes 4 * sin^2(x) - 3 = 0

divide both sides of the equation by 4 to get sin^2(x) - 3/4 = 0

add 3/4 to both sides of the equaton to get sin^2(x) = 3/4

take the square root of both sides of the equation to get sin(x) = plus or minus sqrt(3/4) which is equal to sqrt(3) / sqrt(4) which is equal to sqrt(3) / 2.

you get sin(x) = plus or minus sqrt(3)/2.

you can use your calculator to solve for x, or you can remember that arcsin(sqrt(3)/2) = 60 degrees.

60 degrees * pi / 180 = pi/3 radians.

that's your angle in the first quadrant in radians.

in the second quadrant, the angle is pi - pi/3 = 2/3 * pi = 2pi/3.

in the third quadrant, the angle is pi + pi/3 = 3pi/3 + pi/3 = 4pi/3.

in the fourth quadrant, the angle is 2pi - pi/3 = 6pi/3 - pi/3 = 5pi/3.

since arcsin is plus or minus, then all 4 quadrants apply and you solution is:

x = pi/3, 2pi/3, 4pi/3, 5pi/3 in the interval [0,2pi].

in degrees, that would be x = 60, 120, 240, 300 in the interval [0,360].

i graphed the equation of y = 4 * sin^2(x) - 3 in degrees and radians in the interval [0,360] and [0,2pi].

the graphs are shown below:

$$$

$$$

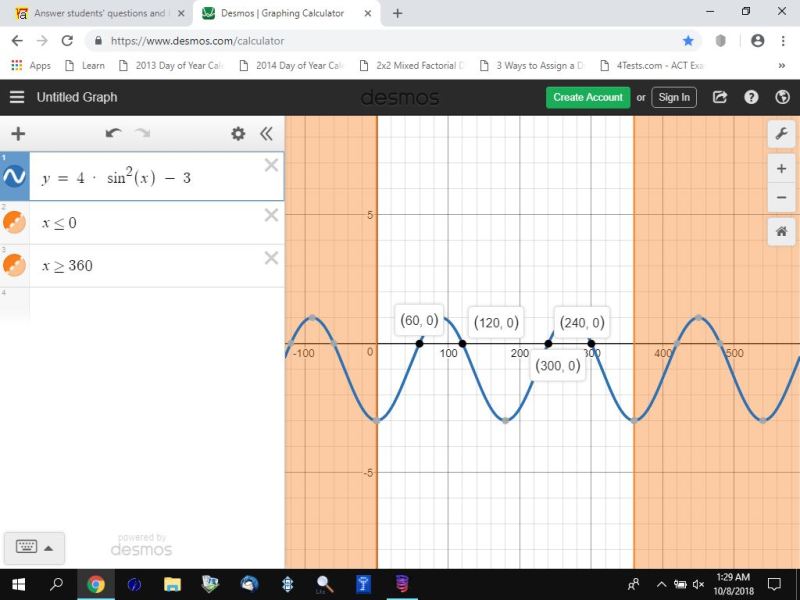
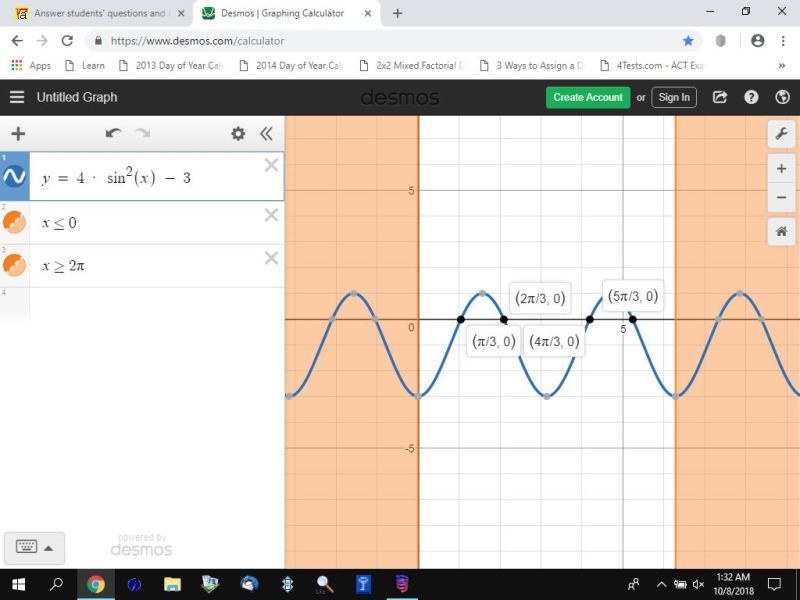
the graph confirms that y = 4 * sin^2(x) - 3 = 0 at those values of x.