convert the angle to degrees and it will be easier to see.
degrees = radians * 180 / pi.
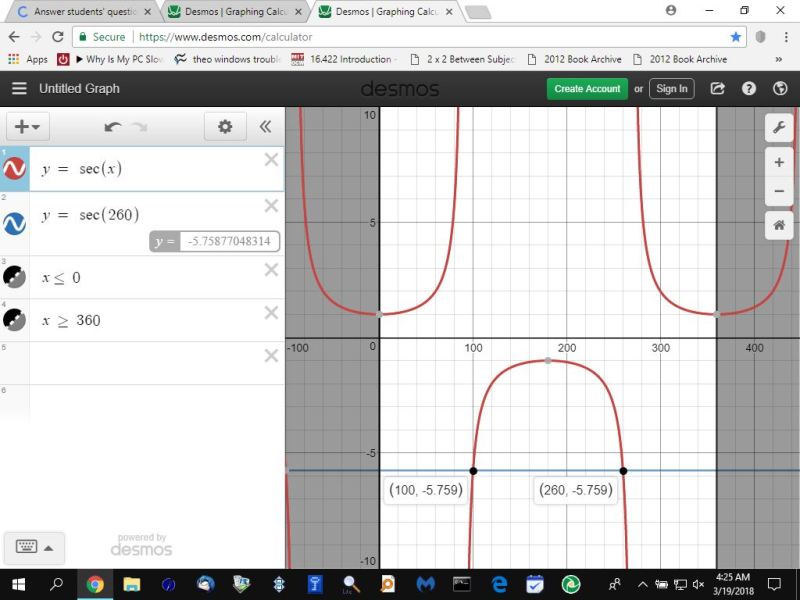
13 * pi / 9 * 180 / pi = 260 degrees.
2 * pi * 180 / pi = 360 degrees.
you are looking for an equivalent angle between 0 and 360 degrees that has the same secant value as 260 degrees.
secant is equal to 1 / cosine.
secant of 260 degrees is equal to 1 / cosine of 260 which is equal to -5.758770483.
your equivalent angle must have a negative secant.
sign of secant follows the sign of cosine.
cosine is positive in the first and fourth quadrants.
cosine is negative in the second and third quadrant.
260 degrees is in the third quadrant.
you are looking for an equivalent angle in the second quadrant.
easiest way to do this is to find the reference angle and then convert the reference angle to an equivalent angle in the second quadrant.
reference angle for an angle in the third quadrant is the angle minus 180.
260 - 180 = 80 degrees.
equivalent angle in the second quadrant is 180 minus the reference angle.
180 - 80 = 100 degrees.
your equivalent angle in the second quadrant should be 100 degrees.
cosine (260) = -.1736481777
cosine (100) = -.1736481777
1/cosine(260) = secant(260) = -5.756770483
1/cosine(180) = secant(100) = -5.758770483
keep in mind that every angle between 0 and 360 degrees will have an equivalent angle in each quadrant.
the equivalent angles will all have the same trig function except for the sign.
the sign is determined by what quadrant the equivalent angle is in.
your angle is 260 degrees.
the equivalent angle in the first quadrant is the reference angle.
from there, you can easily find the equivalent angle in all the other quadrants.
the rules are:
angle in second quadrant = 180 - angle in first quadrant.
angle in third quadrant = 180 + angle in first quadrant
angle in fourth quadrant = 360 - angle in first quadrant.
angle in first quadrant = 180 - angle in second quadrant.
angle in first quadrant = angle in third quadrant - 180
angle in first quadrant = 360 - angle in fourth quadrant.
your angle need to be a positive angle between 0 and 360 degrees to start with.
let's see how these rule apply to your angle.
i'll work in degrees first, and then work in radians.
your angle in radians is 13 * pi / 9.
convert that to degrees to get 13 * pi / 9 radians * 180 / pi = 260 degrees.
you could convert directly to other quadrants except the first quadrant, but i find it easier to convert the angle to the equivalent angle in the first quadrant, which is the reference angle, and then convert to the other quadrants from there.
since you angle is in the third quadrant, you would convert it to the equivalent angle in the first quadrant by using the following rule from the set i showed you above.
angle in first quadrant = angle in third quadrant - 180
260 - 180 = 80 degrees.
that's the equivalent angle in the first quadrant.
from there, you can convert to the other quadrants by suing the following rules from the set i gave you above.
angle in second quadrant = 180 - angle in first quadrant.
180 - 80 = 100 degrees in the second quadrant
angle in third quadrant = 180 + angle in first quadrant
180 + 80 = 260 degrees in the third quadrant
angle in fourth quadrant = 360 - angle in first quadrant.
360 - 80 = 280 degrees in the fourth quadrant.
your equivalent angles between 0 and 360 will be:
80 in the first quadrant
100 in the second quadrant
260 in the third quadrant
280 in the fourth quadrant
since these angles are equivalent, they must all have the same trig functions, except for the sign.
secant(80) = 1 / cosine(80) = 5.758770483
secant(100) = 1 / cosine(100) = -5.758770483
secant(260) = 1 / cosine(260) = -5.758770483
secant(280) = 1 / cosine(280) = 5.758770483
all the trig functions give the same value except for the sign.
you can see that the secant is positive in the first and the fourth quadrant, and that the secant is negative in the second and third quadrant.
your angle is 260 degrees.
the angle with the same secant is 100 degrees.
it has the same value and the same sign.
if you do this in radians, you will get the same result.
the same rules apply, except your angle is in radians rather than degrees.
the rule in radians are:
angle in second quadrant = pi - angle in first quadrant.
angle in third quadrant = pi + angle in first quadrant
angle in fourth quadrant = 2 * pi - angle in first quadrant.
angle in first quadrant = pi - angle in second quadrant.
angle in first quadrant = angle in third quadrant - pi.
angle in first quadrant = 2 * pi - angle in fourth quadrant.
your angle is 13 * pi / 9 radians.
in radians:
the first quadrant is between 0 and pi / 2.
the second quadrant is between pi / 2 and pi.
the third quadrant is between pi and 3 * pi / 2.
the fourth quadrant is between 3 * pi / 2 and 2 * pi.
you're dealing with fractions that have different denominators than your angle and that's a real bummer because it takes more work to get them to the same common denominator.
it's just easier to use your calculator to convert to radians rather than pi radians.
pi / 2 = 1.570796327 radians
pi = 3.141592654 radians
3 * pi / 2 = 4.71238898 radians
2 * pi = 6.283185307 radians
translated, you get:
the first quadrant is between 0 and 1.570796327 radians.
the second quadrant is between 1.570796327 and 3.141592654 radians.
the third quadrant is between 3.141592654 and 4.71238898 radians.
the fourth quadrant is between 4.71238898 and 6.283185307 radians.
your angle is 13 * pi / 9 = 4.537856055 radians.
that puts it in the third quadrant because it is between 3.141592654 and 4.71238898 radians.
now, you just follow the rules as before, except in radians rather than degrees.
angle in first quadrant = angle in third quadrant - pi.
equivalent angle in the first quadrant is 13 * pi / 9 - pi = 1.396263402 radians.
angle in second quadrant = pi - angle in first quadrant.
pi - 1.396263402 = 1.745329252 radians.
angle in third quadrant = pi + angle in first quadrant
pi + 1.396263402 = 4.537856055 radians.
angle in fourth quadrant = 2 * pi - angle in first quadrant.
2 * pi - 1.396263402 = 4.886921906.
your equivalent angle in all 4 quadrants are:
1.396263402 radians in the first quadrant.
1.745329252 radians in the second quadrant.
4.537856055 radians in the third quadrant.
4.886921906 radians in the fourth quadrant.
convert your calculator to radians to get the value of the secant function for these angles.
secant (1.396263402) = 5.758770483
secant (1.745329252) = -5.758770483
secant (4.537856055) = -5.758770483
secant (4.886921906) = 5.758770483
your angle is in the third quadrant.
the equivalent angle that has the same trig function value is in the second quadrant.
that angle is 1.745329252 radians.
the equivalent angle in degrees is that * 180 / pi = 100 degrees.
you get the same answer working in radians as you get working in degrees, but working in degrees is just so much easier.
i usually translate to degrees and then convert my answer back to radians when i'm done.
i have worked directly in radians, but it's harder to visualize and the quadrant boundaries are more difficult to work with.
the concepts and the rules, however, are the same.
here's what the graph looks like in radians.
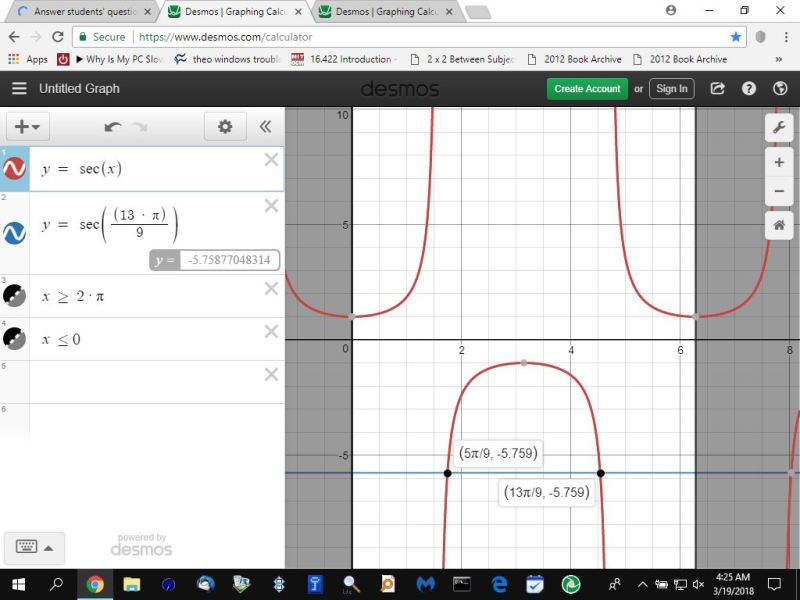
here's what the graph looks like in degrees.
if you converted you angle from * pi / 9 to radians, then you simply divide the result by (pi / 9) to get back to your angle using pi / 9
you will get:
1.745329252 radians / (pi / 9) = 5 * pi / 9 radians
4.537856055 radians / (pi / 9) = 13 * pi / 9 radians.
this is just undoing what you did to get the angle in radians without pi / 9 as a factor.
you started with 13 * pi / 9 and so, you multiplied 13 by (pi/9) to get 4.537856055 radians.
to get back you simply divide by what you multiplied by.
4.537856055 / (pi/9) = 13 * (pi/9)