Question 1029837: Could someone please help me with this problem? I think I may be on the right track, but am not really sure!
"From a squad of 12 cheerleaders, 10 will assemble themselves into a 4-level pyramid.
a) how many different combinations of cheerleaders can be used to build the pyramid? **I think it's 12/10 or 12 C 10 (sub 12, C, sub 10/don't know how to get it on here correctly, sorry!) which equals 66, but I don't understand how to work it out.
b) the coach decides that Alexis must be at the top of the pyramid, and that Rachel, Jen, Britt, and Nicole will form the base. How many different combinations of 10 cheerleaders can now be chosen to form the pyramid?
**I think it's 7/5 and answer is 21, but again I don't know for sure or how to actually arrive at that answer
c) Suppose alexis has an injury and can't participate. the coach replaces Alexis with Rebecca. Now, how many different combinations of 10 cheerleaders can the coach select?
*I think it's 6/5 which equals 6, same on this one, not sure how to work out. Or, if my answers are even correct??
Any help would be appreciated! Thanks!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are originally  cheerleaders that can participate. cheerleaders that can participate.
Of those  , ,  will form a pyramid. will form a pyramid.
The other  will just watch. will just watch.
As the problem's wording suggests, it is a question of combinations (where order/position in the pyramid does not matter).
It is not a question of permutations.
a) The number of different combinations (subsets) of  cheerleaders cheerleaders
that can be made from that set of  available cheerleaders can be calculated by a formula or just reasoned through. available cheerleaders can be calculated by a formula or just reasoned through.
The written and applied formula may be required by the teacher.
Reasoning is all that is needed to get to the solution and/or the formula.
The formula for the number of combinations (subsets) of  objects is objects is
 . .
In this case,
 . .
You could look at it from the other side.
The number of different possible combinations of  cheerleaders to be used to make the pyramid is the same as cheerleaders to be used to make the pyramid is the same as
the number of different possible combinations of  disappointed cheerleaders can be chosen to not participate in the pyramid. disappointed cheerleaders can be chosen to not participate in the pyramid.
Reasoning and calculating the answer that way is easier.
The coach could look at the cheerleaders and decide to leave out the  of them who have missed the most practices. of them who have missed the most practices.
There would be  ways to make his first choice of cheerleader to exclude, ways to make his first choice of cheerleader to exclude,
and  ways to make the second choice. ways to make the second choice.
So the coach's thinking could be made in 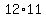 ways when order of choices matter. ways when order of choices matter.
But since the same set of  excluded cheerleaders could be picked excluded cheerleaders could be picked  different ways, different ways,
the number of different possible sets of  excluded cheerleaders is excluded cheerleaders is
 . .
Applying the formula, we would calculate it as

b) Once the coach decide on the  cheerleaders that will be the top and the base of the pyramid, cheerleaders that will be the top and the base of the pyramid,
it is a question of how many different sets of other cheerleaders can the coach choose to form the other two layers to complete the pyramid.
There are still  cheerleaders to choose from for the other cheerleaders to choose from for the other  pyramid positions. pyramid positions.
The number of possible choices is
 . .
You can also reason there are  ways to pick the two cheerleaders who will not participate. ways to pick the two cheerleaders who will not participate.
c)With Alexis injured, there are only  available cheerleaders. available cheerleaders.
Other than that, it is like the situation in part b:
after the coach picks  cheerleaders for specific positions in the cheerleaders for specific positions in the  person pyramid, person pyramid,
there are  more cheerleaders to be chosen more cheerleaders to be chosen
out of the  remaining available cheerleaders. remaining available cheerleaders.
 . .
You can also reason there are  ways to pick the ways to pick the  of the of the  cheerleaders who will not participate. cheerleaders who will not participate.
THE REASONING FOR THE FORMULA:
The reasoning is that when you make the list of the  objects, objects,
there are  possibilities for the first object to be listed, possibilities for the first object to be listed,
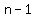 possibilities for the second one, and so on, possibilities for the second one, and so on,
so the list is being built  ways. ways.
The number of ways is a product of consecutive factors counting down from  . .
After the last item is chosen, there are 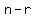 objects not chosen, objects not chosen,
so the final product does not include  , ,
but all the other factors in  are included. are included.
The final product is
 = = , and that is the number of ways the list could be built. , and that is the number of ways the list could be built.
However, a list of  objects can be written objects can be written  different ways, different ways,
because there are  items that could be first, and for each case, there would be items that could be first, and for each case, there would be 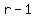 items that could be second, and so on. items that could be second, and so on.
Since the  lists include lists include  repeats of each combination/subset of repeats of each combination/subset of  objects, objects,
the number of combinations of  objects that can be made from a set of objects that can be made from a set of  objects is objects is

|
|
|