SOLUTION: If the area of an isosceles right triangle is equal to the perimeter of a square with an area of 4, what is the ratio of the height of the triangle to the side of the square?

Algebra ->  Triangles -> SOLUTION: If the area of an isosceles right triangle is equal to the perimeter of a square with an area of 4, what is the ratio of the height of the triangle to the side of the square?      Log On


   

Question 577740: If the area of an isosceles right triangle is equal to the perimeter of a square with an area of 4, what is the ratio of the height of the triangle to the side of the square?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The area for a square of side length 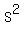S is S%5E2.
If S%5E2=4 ---> S=sqrt%284%29 --> highlight%28S=2%29.
The perimeter, P, of that square is 4 times the length of the side:
P=4%2AS --> P=4%2A2 --> highlight%28P=8%29
The area, A, of any triangle is calculated from a base and the corresponding height as
A=base%2Aheight%2F2
As a triangle has 3 sides, any of them can be considered the base. We chose, trying to make calculations as easy as possible.

An isosceles right triangle has two legs of equal length (L in the figure above) forming a right angle.
When calculating the area of an isosceles right triangle, it makes sense to consider one of the legs the base of the triangle, making the length of the other leg the height of the triangle. (It is so easy to calculate the area that way, that one could easily forget that we can turn that triangle around, like on the right side of the figure above, and consider the hypotenuse to be the base).
If the length of each leg is L, then the area, A, of the triangle is
A=L%5E2%2F2
The problem says that the area of the triangle is equal to the perimeter of the square, so A=P, and
L%5E2%2F2=8 --> L%5E2=2%2A8=16 --> L=sqrt%2816%29 --> highlight%28L=4%29
So, if what is understood by height of the isosceles right triangle is L,
the ratio of height of the triangle to the side of the square is
L%2FS=4%2F2 --> highlight%28L%2FS=2%29
and that is probably the expected answer.
IF IT IS A TRICK QUESTION
then you are supposed to consider the "other height." That other height is the green line in the triangle on the right side of the drawing above, where the hypotenuse is considered to be the base.
According to Pythagoras, the length of the hypotenuse, is
sqrt%28L%5E2%2BL%5E2%29=sqrt%282L%5E2%29=sqrt%282%29%2Asqrt%28L%5E2%29=L%2Asqrt%282%29
As you see, the green line divides the triangle into two similar triangles, with legs length equal to half of the hypotenuse length, or L%2Asqrt%282%29%2F2.
One of those legs is the green line height.
In your triangle, with L=4,that height would be
4%2Asqrt%282%29%2F2=2sqrt%282%29
and the ratio of that height to the length of the side of the square would be
2sqrt%282%29%2F2=sqrt%282%29
So the answer to the trick question would be that the ratio of the height of the triangle to the side of the square depends on which side of the triangle you call base.
If you call one of the legs base, the other leg is an altitude and the ratio is 2.
If you call the hypotenuse base, then the calculations get a bit more complicated, and the ratio is sqrt%282%29