SOLUTION: Use algebraic rules of equations to predict the solution type to the system of equations f(x)={x+y=-4 y=2x-1

Question 1203037: Use algebraic rules of equations to predict the solution type to the system of equations
f(x)={x+y=-4 y=2x-1
Found 3 solutions by josgarithmetic, Theo, ikleyn:
Answer by josgarithmetic(39618)   (Show Source): You can put this solution on YOUR website!
Exactly ONE solution

You can decide what rules you need, but two lines intersecting at exactly one single point. Exactly ONE solution.
Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
here's what i get.
your equations that need to be solve simultaneously are:
x + y = -4
y = 2x - 1
we'll use the substitution method.
in the first equation, replace y with 2x - 1 from the second equation to get:
x + 2x - 1 = -4
add 1 to both sides of the eeuation and combine like terms to get:
3x = -3
solve for x to get x = 1-1
in the second equation, replace x with -1 and solve for y to get:
y = 2*-1 - 1 = -3
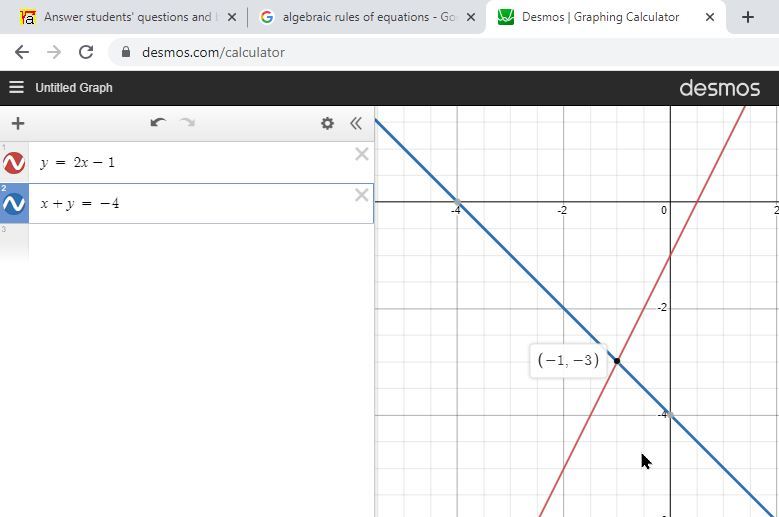
your solution to this equation is x = -1 and y = -3
replace x with -1 and y with -3 in both equations to ge:
x + y = -4 becomes -1 + -3 = -4 which becomes -4 = -4 which is true.
y = 2x - 1 becomes -3 = 2*-1 - 1 which becomes -2 -1 = -3 which becomes -3 = -3 which is true.
both equations are true when x = -1 and y = -3.
the graph of these equations is shown below.

A system of simultaneous linear equations can have either: one unique solution, infinitely many solutions or no solutions.

from a graphical standpoint, the unique solution is where the lines intersect; infinitely many solution are when the lines are identical, i.e. both equations form the same equivalent equation which generates the same line for both; no solutions are whn the lines are parallel to each other.

theee are ptjer waus to describe the solutions as noted in the following reference.
https://ionamaths.weebly.com/uploads/1/4/2/0/14204419/consistencyanddependency.pdf

i think that about covers it.
let me know if you need more.
theo

Answer by ikleyn(52788)   (Show Source): You can put this solution on YOUR website!
.

How the problem is formulated, it is either bad translation or bad unprofessional composition,
or a copy-paste from a bad source.

It does not sound as a right Math composition.

The first wish when reading this post, is to plug the ears with cotton so that do hear nothing.

RELATED QUESTIONS
Use algebraic rules of equations to predict the solution type to the system of equations (answered by greenestamps,ikleyn)
Use algebraic rules of equations to predict the solution type to the system of equations (answered by Alan3354)
find the solution to the system of equations: x+y=1 and... (answered by solver91311)
Find a solution to the system of equations by graphing. 2x-y=8... (answered by mananth)
Find the solution to the system of equations. x + y = 4 and y = 2x + 1 I... (answered by rfer)
What is the solution to the system of equations? 2x+y=-3... (answered by TimothyLamb,Fombitz)
What is the solution to the following system of equations? 2x+3y=6... (answered by checkley77)
what is the solution of the following system of equations? y=x+4... (answered by Fombitz)
What is the solution to the system of equations? x + y = 2 x - y =... (answered by MathLover1)