The base is square.
The height is 6.
The lateral edge is 10.
Here's a reference that tells you all sorts of things related to pyramids.
One of those things describes what the lateral edge is and tells you how to calculate it given the radius of the base and the height.
http://www.vitutor.com/geometry/solid/pyramid_math.html
In your problem, you are given the height and the lateral edge and you are asked to find the slant height.
That's slightly different.
The slant height would be the altitude of any of the lateral faces.
Lateral face and slant face are the same as far as I can tell.
Check the reference for a description of what a lateral face is.
To find the slant height, you need to find the apothem of the base.
To find the apothem of the base, you need to find the radius of the base.
the picture below shows you what your pyramid will look like.

AE is a lateral edge.
AB is the height of the pyramid.
BE is radius of the base of the pyramid. If you were to circumscribe a circle around the base of the pyramid, BE would be the radius of that circle.
BG is the apothem of the base of the pyramid. If you were to inscribe a circle within the base of the pyramid, BG would be the radius of that circle.
Angle x is the angle that you need to find the radius of the base.
Angle x is angle AEB.
The sine of angle x is equal to opposite / hypotenuse which is equal to AB / AE which is equal to 6/10 which is equal to .6
Angle x is equal to arcsine of .6 which is equal to 36.86989765 degrees.
Cosine of angle x is equal to adjacent / hypotenuse which is equal to BE / AE which is equal to BE / 10.
Multiply both sides of this equation by 10 and you get 10 * cosine of angle x is equal to BE.
This makes BE equal to 8 as shown in the diagram.
You now have enough information to find BG which is the apothem of the base.
In order to find the apothem of the base, you need to know what angle y is.
angle y is angle BEG.
Since the base is a square, angle y is equal to 45 degrees.
The sine of angle y is equal to opposite / hypotenuse which is equal to BG / BE which is equal to BG / 8.
Multiply both sides of this equation by 8 to get:
8 * sine (45) = BG.
This makes BG equal to 5.65685425.
You now have enough information to find the slant height.
In order to do that, you need to find angle z.
Angle z is angle AGB.
The tangent of angle z is equal to opposite / adjacent which is equal to AB / BG which is equal to 6 / 5.65685425 which is equal to 1.060660172.
The arc tangent of 1.060660172 is equal to 46.68614334.
Angle y is equal to 46.68614334.
You can now find the slant height.
The sine of angle z is equal to opposite / hypotenuse which is equal to AB / AG which is equal to 6 / AG.
Multiply both sides of this equation by AG and divide both sides of this equation by sine (z) to get:
AG = 6 / sine(z)
Since z equals 46.68614334 degrees, this equation becomes:
AG = 6 / sine (46.68614334) which is equal to 6 / .727606875 which is equal to 8.246211251.
AG is equal to 8.246211251 which is equal to the slant height of your pyramid.
The following picture shows you the details of each section of the pyramid as we progress from the start to the solution.
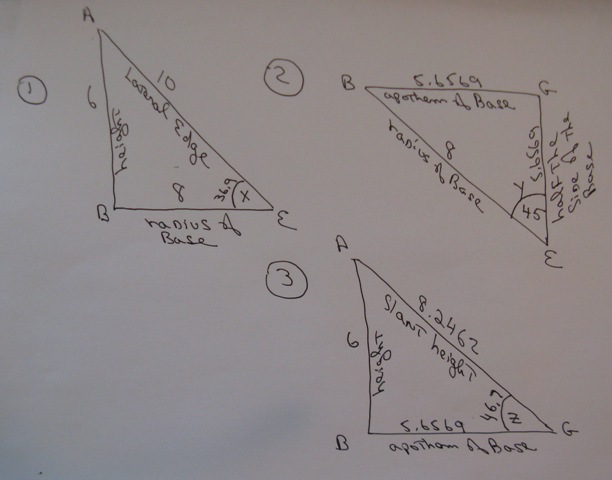
Step 1 is where we find the radius of the base.
Step 2 is where we find the apothem of the base.
Stepo 3 is where we find the slant height of the pyramid.