Lesson Area of a circle

Algebra ->  Surface-area -> Lesson Area of a circle      Log On


   

This Lesson (Area of a circle) was created by by ikleyn(52781) About Me : View Source, Show
About ikleyn:

Area of a circle


The area of a circle  S  equals

S = pi.r%5E2,   or   S = pi%2Ad%5E2%2F4,               (1)

where  r  is the circle radius,  d  is the circle diameter,  and  pi  is the constant            
value equal to the ratio of the circle circumference length to the circle diameter.

The number  pi  is a transcendental number.  Its approximate value is
    pi =~ 3.14            with two digits after the decimal point,  or
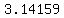    pi =~ 3.14159       with five digits after the decimal point,  or
    pi =~ 3.14159265  with eight digits after the decimal point.


Figure 1.   Area of a circle

Example 1

Find the area of a circle which has the radius of  10 cm.

Solution

Use the formula above for the area of a circle via its radius.  It gives
S = pi.r%5E2 = 3.14159%2A10%5E2 = 3.14159%2A100 = 314.159 cm%5E2.

Answer.  The area of the circle is  314.159 cm%5E2.


In the school geometry,  the formula  (1)  for the circle area is considered as granted,  without proof.
The proof of the formula  (1)  can be found in courses of  Calculus.

The arguments below aim to help you understand why the formula  (1)  is true.

From the lesson  Area of n-sided polygon circumscribed about a circle  you know that the area                  
of a polygon circumscribed about a circle  S%5Bp%5D  is equal to the half product of the polygon's
perimeter  P  and the radius of the circle  (Figure 2):   S%5Bp%5D = 1%2F2.P.r.

Now,  if you increase the number of sides of the circumscribed polygon in a way that its
side measures will uniformly decrease,  you will get the area of polygons closer and closer
to the area of the circle and the perimeter of polygons closer and closer to the
circumference of the circle.  In this way you will get the formula  (1).

The next line presents this chain of arguments in the short form:



  Figure 2.  To the  Theorem 1        

S%5Bp%5D = 1%2F2.P.r   //   S%5Bp%5D ---> S, P ---> 2%2Api%2Ar   //   ===> S = 1%2F2.2%2Api%2Ar.r = pir%5E2.


Problem 1

Find the area of a ring concluded between two concentric circles that have the radii of  10 cm  and  6 cm.

Solution

We are given two concentric circles that have the common center  (Figure 3).              
The larger circle has the radius of  R = 10 cm  and  the smaller circle has the
radius of  r = 6 cm.  We need to find the area of the ring concluded between
these two circles.

The larger circle has the area   S = pi%2AR%5E2 = 3.14159%2A100 = 314.159 cm%5E2.
The smaller circle has the area   s = pi%2Ar%5E2 = 3.14159%2A36 = 113.097 cm%5E2.
The area of the ring is the difference of the areas of the circles:
S%5Bring%5D = S - s = 314.159 - 113.097 = 201.062 cm%5E2.


Figure 3.  To the  Problem 1

Answer.  The area of the ring is  201.062 cm%5E2.


Problem 2

Find the area of the circle which is inscribed in the  60°-sector of the circle with the radius of  12 cm.

Solution

We are given a  60°-sector of the circle with the radius of  12 cm  and the              
smaller circle,  which is inscribed in the sector  (Figure 4a).              
The smaller circle touches the radii of the sector,  as well as the larger
circle  (Figure 4a).  We need to find the area of the smaller circle.

Let us draw the angle bisector  OB  of the given sectorial angle of  60°
(Figure 4b),  where the point  B  lies on the larger circle.  It is clear that
the angle bisector  OB  passes through the center  A  of the inscribed
circle.  It is also clear from the symmetry that the point  B  is the
tangent point of the two circles.



Figure 4a. To the Problem 2    




Figure 4b. To the solution
      of the Problem 2

Now,  since the angle  LCOA  is of 30°,  the hypotenuse  OA  is twiced the leg  AC:  |OA| = 2r.  Therefore,  R  is tripled the radius  r:
R = |OA| + r = 2r + r = 3r.

In other words,  r = R%2F3.  Hence,  in our case,  r = 12%2F3 = 4 cm.
It implies that the area of the smaller circle is  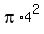pi%2Ar%5E2 = pi%2A%28R%2F3%29%5E2 = pi%2A4%5E2 = 3.14159%2A16 = 50.265 cm%5E2.
Answer.  The area of the smaller circle is  50.265 cm%5E2.


My other lessons on the area of a circle,  the area of a sector and the area of a segment of the circle in this site are
    - Area of a sector  and
    - Area of a segment of the circle
under the current topic  Area and surface area  of the section  Geometry,  and
    - Solved problems on area of a circle,
    - Solved problems on area of a sector,
    - Solved problems on area of a segment of the circle  and
    - Solved problems on area of a circle, a sector and a segment of the circle
under the topic  Geometry  of the section  Word problems.

To navigate over all topics/lessons of the Online Geometry Textbook use this file/link  GEOMETRY - YOUR ONLINE TEXTBOOK.

This lesson has been accessed 2933 times.