Question 703765: Hello I need help in finding the sum of 101+102+103+ . . .+ 500. As in my previous question, I know the answer which is 500+101, 499+102, 498+103, ...=601 which we then multiply by 200 (400/2) and it equals 120,200 every time we do this calculation with the listed above numbers. But how to put it in the formula that will work for this problem as well as for my first question how to find the sum of first 500 integers?
Thank you for help.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! S=(101+102+103+ . . . + 498+499+500) is the sum of 400 terms of an arithmetic sequence (called arithmetic progression in some places).
Consecutive terms of an arithmetic sequence/progression differ by the same number, called the "common difference".
In this case, the common difference is 1.
Because of that, if the first term is  ,
the last term is  , and the common difference is  ,
the second term is  ,
and the second-to-last term is 
Adding terms head-to-tail, we get the same sums
first + last =  and
second + second-to-last =  .
I know that you worry about what to do if there is an odd number of terms.
The answer is to "clone" the sum.
If you had s=(101+102+103+104+105), with an odd number of terms, just 5 terms.
Its "evil twin" is
s=(105+104+103+102+101)
To get an even number of term, that can be grouped into pairs we calculate 2S = S + S =
(101+102+103+104+105) +
(105+104+103+102+101) =
(101+105)+(102+104)+(103+103)+(104+102)+(105+101)= 206+206+206+206+206=5*206
Then we divide by 2:
2s = 5*206 --> 2s/2 = 5*206/2 --> s=5*206/2=515
Back to our arithmetic sequence/progression
The sum of the  term is
 + . . . +
 + . . . +
 + . . . +
 -->  --> 
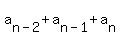
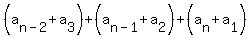
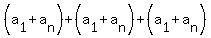
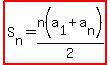
So 101+102+103+ . . . +498+499+500=400(101+500)/2=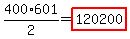
1+2+3+ . . . + 498+499+500=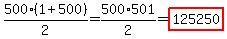
(It's not 125,500)
1+2+3+ . . . +498+499=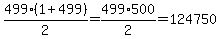
When it's the sum of the first n consecutive integers, it's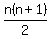 
Either n, or n+1 is an even number, so you always get an integer sum.
If you do not know the value for ,
you can calculate it from , and
as 
You can also calculate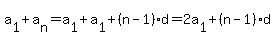 
and use that to make an even more impressive formula for the sum:
|
|
|
