SOLUTION: The product of three consecutive terms in a geometric sequence is -1000, and their sum is 15. Find the common ratio.

Algebra ->  Sequences-and-series -> SOLUTION: The product of three consecutive terms in a geometric sequence is -1000, and their sum is 15. Find the common ratio.       Log On


   

Question 439410: The product of three consecutive terms in a geometric sequence is -1000, and their sum is 15. Find the common ratio.
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
Let a, ar, and 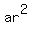ar%5E2 be the terms in geometric sequence.
Then from the given, a%2Aar%2Aar%5E2+=+a%5E3r%5E3+=+%28ar%29%5E3+=+-1000, or ar = -10, after taking cube roots.
==> a = -10/r.
Also, a+%2B+ar+%2B+ar%5E2+=+15<==> a%281%2Br%2Br%5E2%29+=+15
<==> %28-10%2Fr%29%281%2Br%2Br%5E2%29+=+15
<==> 0+=+r%5E2+%2B+5r+%2B+2, after cross-multiplying and simplifying.
<==> (2r+1)(r+1) = 0
==> r = -1/2 or -2
==> a = 20 or 5, respectively.
Hence the sequences are {20, -10, 5} and { 5, -10, 20}. (The two sequences are DIFFERENT because they have different first terms and common ratios.)