SOLUTION: Find the sum of the infinite series (if it exists) <img src="http://i293.photobucket.com/albums/mm56/cool_user2004/7-1.png" alt="Photobucket

SOLUTION: Find the sum of the infinite series (if it exists) <img src="http://i293.photobucket.com/albums/mm56/cool_user2004/7-1.png" alt="Photobucket - Video and Image Hosting">

Question 172793: Find the sum of the infinite series (if it exists)

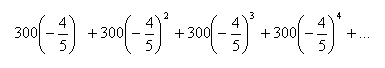
Answer by jim_thompson5910(35256) (Show Source): You can put this solution on YOUR website!
Take note that the terms form a geometric sequence (since there is a common ratio and exponent involved)

Recall, the formula for a geometric sequence is where

Since the coefficient is 300, this tells us that

Since the value being raised to a power is , this means that

So the formula is . So, for instance, if , then (which is the third term).

Also, remember that the formula for an infinite geometric series is

Since we're starting at n=1, the series needs to be rewritten to

So in this case, the formula we'll use is

So the sum of the infinite series is
RELATED QUESTIONS
Find the sum (answered by jim_thompson5910)
Find the general term and the 29th term of the sequence (answered by jim_thompson5910)
Find the 4th term of the given sequence (simplify completely). (answered by jim_thompson5910)
Find the solution of the system of inequalities (answered by jim_thompson5910)
Find the missing length of the right triangle (answered by jim_thompson5910)
(answered by jim_thompson5910)
6. Find the missing angle. (answered by jim_thompson5910)
7. Find the measure of angle x and measure of angle y. (answered by jim_thompson5910)
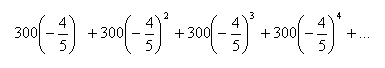
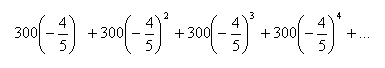
4. The two triangles are similar. Find the indicated side. Find y. (answered by jim_thompson5910)