|
Question 1200515: Find the arithmetic sequence which has the sum of its n terms equal to 2n^2+3n
Thank you
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the arithmetic sequence which has the sum of its n terms equal to 2n^2+3n
~~~~~~~~~~~~~~~~~~~~~~~
To solve this problem, you need to know that
+----------------------------------------------------+
| the sum of any arithmetic progression is |
| a quadratic function of the index "n", |
+----------------------------------------------------+
and vice versa,
+----------------------------------------------------+
| any quadratic function of the integer index "n" |
| creates a unique arithmetic progression. |
+----------------------------------------------------+
Based on these facts, it is enough to find the first term of the progression
and the second term, and then calculate its common difference.
n= 1: 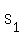 = 2*1^2+ 3*1 = 5. = 2*1^2+ 3*1 = 5.  = 5.
n= 2: = 5.
n= 2: 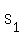 = 2*2^2+ 3*2 = 14. = 2*2^2+ 3*2 = 14.  = = 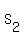 - - 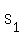 = 14 - 5 = 9.
This arithmetic progression has the first term = 14 - 5 = 9.
This arithmetic progression has the first term  = 5 and the common difference d= = 5 and the common difference d=  - -  = 9 - 5 = 4.
The progression is 5, 9, 13, 17, . . . = 9 - 5 = 4.
The progression is 5, 9, 13, 17, . . .
Solved.
-------------------
On these properties of arithmetic progression, learn from the lessons
- Free fall and arithmetic progressions
- Uniformly accelerated motions and arithmetic progressions
- Increments of a quadratic function form an arithmetic progression
in this site.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 5, 9, 13, 17, 21, ...
Starting term = 5
Common difference = 4
The nth term formula is a(n) = 5+4*(n-1) which fully simplifies to a(n) = 4n+1
Explanation:
Sn = sum of the first n terms
Sn = 2n^2 + 3n
This was given to us in the instructions.
If n = 1, then Sn = S1 = the first term of the arithmetic sequence.
Let's find that first term.
Sn = 2n^2 + 3n
S1 = 2*1^2 + 3*1
S1 = 2*1 + 3*1
S1 = 2 + 3
S1 = 5
The first term of the arithmetic sequence is 5.
Now let's find S2
Sn = 2n^2 + 3n
S2 = 2*2^2 + 3*2
S2 = 2*4 + 3*2
S2 = 8 + 6
S2 = 14
This represents the sum of the first two terms. We'll use it to determine what the second term would be:
S2 = term1+term2
14 = 5+term2
term2 = 14-5
term2 = 9
The arithmetic sequence so far is 5,9,...
This is sufficient info to determine the common difference
d = term2-term1
d = 9-5
d = 4
So we have:
a1 = first term = 5
d = common difference = 4
The nth term formula is:
a(n) = a1 + d*(n-1)
a(n) = 5 + 4*(n-1)
a(n) = 5 + 4n-4
a(n) = 4n + 1
Check:
| n |  |  (method 1) (method 1) |  (method 2) (method 2) | | 1 | 5 | 5 | 2n^2+3n = 2*1^2+3*1 = 5 | | 2 | 9 | 5+9 = 14 | 2n^2+3n = 2*2^2+3*2 = 14 | | 3 | 13 | 5+9+13 = 27 | 2n^2+3n = 2*3^2+3*3 = 27 | | 4 | 17 | 5+9+13+17 = 44 | 2n^2+3n = 2*4^2+3*4 = 44 | | 5 | 21 | 5+9+13+17+21 = 65 | 2n^2+3n = 2*5^2+3*5 = 65 |
The two  columns have their results match up, so this helps confirm the answer. columns have their results match up, so this helps confirm the answer.
Another way to check:
 One formula to quickly find the sum of the first n terms of an arithmetic sequence One formula to quickly find the sum of the first n terms of an arithmetic sequence
 Plug in the first term of 5 Plug in the first term of 5
 Plug in the nth term formula of a(n) = 4n+1 Plug in the nth term formula of a(n) = 4n+1


 Therefore, the answer is confirmed. Therefore, the answer is confirmed.
Arguably this is better confirmation compared to the table of examples as shown above
Another possible arithmetic summation formula to use would be  . .
Plug in  and and  . Simplifying should lead to . Simplifying should lead to 
I'll let you do this verification pathway.
|
|
|
| |