.
The basic solutions are these 5 triples:
a b c
-------------------
0 0 15 (1)
0 9 12 (2)
2 5 14 (3)
2 10 11 (4)
5 10 10 (5)
1) Triple (1) creates 3 permutations, that are the solutions, too.
Playing with the signs, each of these permutations provides 2 triples, that are the solutions, too.
So, the triple (1) produces 2*3 = 6 triples that are the solutions.
2) Triple (2) creates 6 permutations, that are the solutions, too.
Playing with the signs, we get  = 24 triples, that are the solutions, too.
So, the triple (2) produces 24 triples that are the solutions.
3) Triple (3) creates 6 permutations, that are the solutions, too.
Playing with the signs, each of these permutations provides 2 triples, that are the solutions, too.
So, the triple (3) produces
= 24 triples, that are the solutions, too.
So, the triple (2) produces 24 triples that are the solutions.
3) Triple (3) creates 6 permutations, that are the solutions, too.
Playing with the signs, each of these permutations provides 2 triples, that are the solutions, too.
So, the triple (3) produces 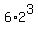 = 48 triples that are the solutions.
4) Triple (4) creates 6 permutations, that are the solutions, too.
Playing with the signs, each of these permutations provides 2 triples, that are the solutions, too.
So, the triple (4) produces
= 48 triples that are the solutions.
4) Triple (4) creates 6 permutations, that are the solutions, too.
Playing with the signs, each of these permutations provides 2 triples, that are the solutions, too.
So, the triple (4) produces 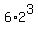 = 48 triples that are the solutions.
5) Triple (5) creates 3 permutations, that are the solutions, too.
Playing with the signs, each of these permutations provides 2 triples, that are the solutions, too.
So, the triple (4) produces
= 48 triples that are the solutions.
5) Triple (5) creates 3 permutations, that are the solutions, too.
Playing with the signs, each of these permutations provides 2 triples, that are the solutions, too.
So, the triple (4) produces 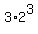 = 24 triples that are the solutions.
= 24 triples that are the solutions.
In all, there are 6 + 24 + 48 + 48 + 24 = 150 different integer triples that are the solutions.