SOLUTION: Hello, I am kind of stumped at how I need to approach this problem. I'm fairly sure that you have to use sequences to solve this, but I am unsure of how to write it down to even be

Question 1085040: Hello, I am kind of stumped at how I need to approach this problem. I'm fairly sure that you have to use sequences to solve this, but I am unsure of how to write it down to even begin to solve it. I hope this isn't too confusing to read, but it's the only way I can type it out. I appreciate any time and effort that you put into this to solve it.
Thanks in advance for your help!

Anthony is an astrobiologist studying a spherical alien organism that replicates itself when exposed to dihydrogen monoxide. The initial organism has a radius of 4 Mum (a Mum is one-millionth of a meter).
When exposed, it grows 4 similar copies of itself, tangent to and equally 1 spaced around the parent organism, but with only 1/ 4 the radius.
As the exposure continues, each member of the successive generations grows 4 additional copies of itself, each with 1/4 the radius of the prior generation.
This growth, diagrammed below, will continue for as long as exposure continues.
Table------------------------
Generation / New spheres / New Surface Area Added / New Volume Addded
1 ------------------------ 1 ------------------------ 64pi ------------------------ 256pi/3
2 ------------------------ 4 ------------------------ 16pi ------------------------ 16pi/3
3
4
n
30. Find the combined surface area of all the organisms as n tends to infinity, if possible.
31. Find the combined volume of all the organisms as n tends to infinity, if possible. Recall that for a sphere with radius r, the surface area SA = 4pir^2, and the volume = 4.3pir^2
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
this is a geometric series.

the formula for sum of the surface area becomes Sn = 64 * pi * (1 - (1/4)^n) / (1 - (1/4))

the formula for the sum of the volume becomes Sn = (256/3) * pi * (1 - (1/16)^n) / (1 - 1/16)

the formula for each succeeding surface area becomes An = 64 * pi * (1/4)^(n-1)

the formula for each succeeding volume becomes An = (256/3) * (1/16)^(n-1)

i tested these formulas out using excel and they agree with what each of the values should be.

you can test these formulas out for n = 1 through 4 and you'll see that they work.

my excel worksheet for doing it manually through finding the number of spheres and the radius of each of the spheres is sh own below.

$$$

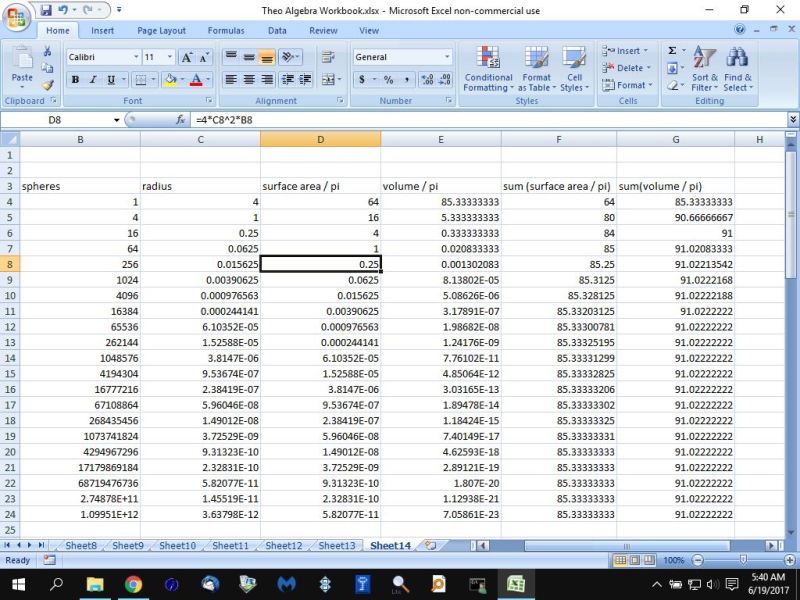
my excel worksheet for doing it via the formulas is shown below:

$$$

the numbers match.

if my assumptions were right about what you were looking for, then the formulas are right.

i don't have time to go through the derivation of the formulas right now, but if you want or need to know, then send me an email and i'll work them up for you.

notice the excel worksheet gives the results as being divided by pi.

this means the actual result is what is shown * pi.

therefore, if you see 16 as a result, it's really 16 * pi, etc.

RELATED QUESTIONS
Hey, I am confused with this word problem in which I have to use arithmetic/geometric... (answered by jim_thompson5910)

I really need help trying to figure this out. I don't want an answer I just need help... (answered by stanbon)

Hello! I am confused with this word problem in which I have to use geometric/arithmetic... (answered by rfer)

Hello. I am in need of help on this problem: Use a calculator to approximate Square... (answered by stanbon)

Hi,I have a problem not sure how to approach it. 4s-7+=-2(1-s) (answered by Nate)

We have recently started working with finding vertical asymptotes in class and I came... (answered by MathLover1)

Hello! I have a question concerning the following problem. I know your supposed to use... (answered by longjonsilver)

This is the problem: Use unit multipliers to convert 16,000 inches to miles. I am... (answered by funmath,checkley71)

Hello, I am stuck on a mixture word problem. We have to use 2 unknowns (i.e., Let x=___... (answered by scott8148)