Question 1069603: Three consecutive terms in an arithmetic sequence is given with a middle one x. The sum of the three terms is 30 and the product of the three terms is 840
Calculate the three terms
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Three consecutive terms in an arithmetic sequence is given with a middle one x. The sum of the three terms is 30 and
the product of the three terms is 840. Calculate the three terms
~~~~~~~~~~~~~~~~~~~
The terms are x-d, x and x+d, where d is the common difference.
For x, you have the equation
(x-d) + x + (x+d) = 30,
which is equivalent to
3x = 30
and gives x = 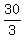 = 10.
The second equation is
(x-d)*x*(x+d) = 840, or
(10 - d)*10*(10 + d) = 840,
which gives = 10.
The second equation is
(x-d)*x*(x+d) = 840, or
(10 - d)*10*(10 + d) = 840,
which gives
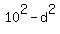 = = 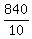 , or , or
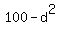 = 84, ---> = 84, --->  = 100 - 84 = 16, ---> = 100 - 84 = 16, --->  = 4, = 4,  = -4.
The first progression is {6, 10, 14}.
The second progression is {14, 10, 6}. = -4.
The first progression is {6, 10, 14}.
The second progression is {14, 10, 6}.
There is a bunch of lessons on arithmetic progressions in this site
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- Chocolate bars and arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Arithmetic progressions".
|
|
|