Question 1038972: For a given geometric sequence, the 5th term, a5, is equal to 11/256, and the 10th term, a10, is equal to −44. Find the value of the 12th term, a12. If applicable, write your answer as a fraction.
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For a given geometric sequence, the 5th term, a5, is equal to 11/256, and the 10th term, a10, is equal to 44.
Find the value of the 12th term, a12. If applicable, write your answer as a fraction.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Take the ratio  = =  = =  = 1024 = = 1024 =  . .
Take the 5-degree root of this ratio:  = = 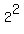 = 4. = 4.
It is your  , the common ratio. , the common ratio.
Then multiply  by by  . .
You will get  = =  . .
It is your answer.
As the last step, think, why it is correct.
Your lesson on geometric progressions is Geometric progressions in this site.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! For a given geometric sequence, the 5th term, a5, is equal to 11/256, and the 10th term, a10, is equal to −44. Find the value of the 12th term, a12. If applicable, write your answer as a fraction.
Common ratio: - 4
12th term, or 
|
|
|