let l = the length
perimeter = l + 3w
the perimeter is equivalent to the amount of fencing required.
because the property is divided into two pieces, there are 3 widths rather than 2, the third width being the partition in the middle.
since perimeter = 2400, the formula for perimeter becomes:
2400 = l + 3w
the area formula is:
area = l * w
this is the area of the enclosure which includes both halves.
since 2400 = l + 3w, we can solve for l to get l = 2400 - 3w
formula for area = l * w becomes area = (2400 - 3w) * w
remove parentheses to get area = 2400w - 3w^2
this is a quadratic equation.
rearrange the terms to get area = -3w^2 + 2400w
set this equation to 0 to get -3w^2 + 2400w = 0
this is in standard quadratic equation form of aw^2 + bw + c = 0
a is the coefficient of the w^2 term, b is the coefficient of the w term, c is the constant term.
we get:
a = -3
b = 2400
c = 0
the formula for the value of w that provides maximum point on this equation is:
w = -b/2a
the maximum point on this equation is the maximum area of the enclosure.
this results in w = -2400 / -6 which is equal to 400.
the area is maximized when w = 400.
when w = 400, the area is equal to 2400w - 3w^2 which becomes 2400*400 - 3*400^2 which results in an area of 480,000 square yards.
when w = 400, l = 1200 because 2400 = 1200 + 3 * 400.
your solutions are:
perimeter = 2400 = l + 3w
area = l*w
area = (2400 - 3w) * w which is equal to 2400w - 3w^2.
largest area is when w = 400 and l = 1200.
w is the width of the enclosure.
l is the length of the enclosure.
l is the letter L, not to be confused with 1 which is the number one.
they are unfortunately very close in appearance with the number 1 having a slanted tip on the top while the letter l has a horizontal tip on the top.
otherwise they are identical.
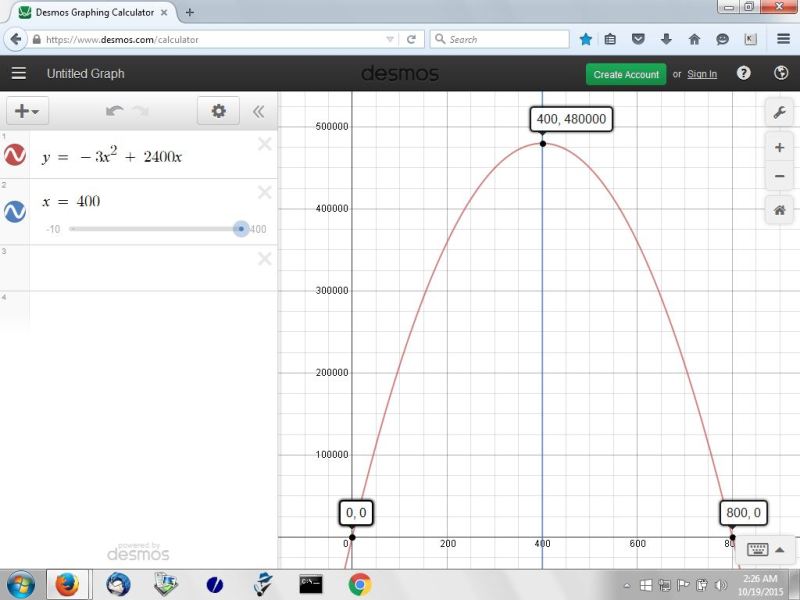
here's a graph of the equation for the area so you can see what the qaution looks like when graphed.
to graph the equation, the area is represented by y and the width is represented by x.
it's easy to see from the graph that the maximum area is when x = 400.