SOLUTION: An engineer constructs side-by-side parabolic arches to support a bridge over a road and a river. The arch over the road has a maximum height of 6 m and a width of 16 m. The river

Question 934652: An engineer constructs side-by-side parabolic arches to support a bridge over a road and a river. The arch over the road has a maximum height of 6 m and a width of 16 m. The river arch has a maximum height of 8 m, but its width is reduced by 4 m because it intersects the arch over the road. Without this intersection, the river arch would have a width of 24 m. A support footing is used at the intersection point of the arches. The engineer sketched the arches on a coordinate system. She placed the origin at the left most point of the road.
(24, 8)
(8, 6)
a) Determine the system of equations that models the two arches.
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
the system of equations will be:

y1 = -6/64 * x^2 + 96/64 * x

y2 = -8/144 * x^2 + 384 / 144 * x - 3456 / 144

if you graph those equations, you will get:

$$$

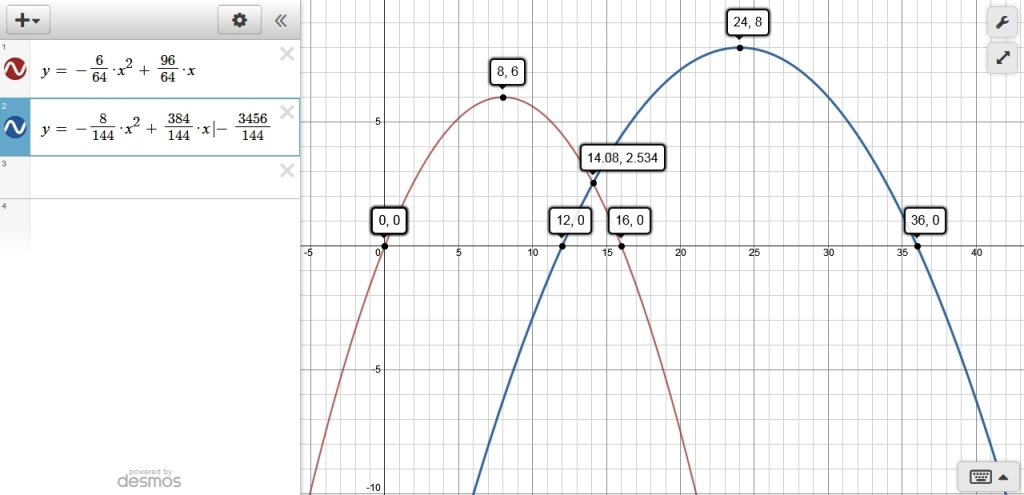
the first equation is modeled by knowing that the zeroes of that eqution are at x = 0 and x = 16.

this means the factors of that equation are (x-0) * (x-16) = 0 which becomes x^2 - 16x = 0

the general equation becomes y = a * (x^2 - 16x)

you know that y = 6 when x = 8, so replace x in that equation to get a * (8^2 - 16(8)) = 6 which becomes a * (-64) = 6 which becomes -64*a = 6 which becomes a = -6/64.

your equation of y = a * (x^2 - 16x) becomes y = -6/64 * (x^2 - 16x) which becomes y = -6/64 * x^2 + 96/64 * x

that's the first equation that was graphed.

the second equation was solved for in a similar manner.

the roots were 12 and 36
the factors were (x-12) * (x-36) = 0
multiplying those factors out got x^2 - 48x + 432 = 0
the general equation became y = a * (x^2 - 48x + 432)
when x was 24, y was 8, so we got 8 = a * (24^2 - 48*24 + 432) which became 8 = 576 * a - 1152 * a + 432 * a which became 8 = -144 * a
divide both sides of that equation by -144 and you get a = -8/144.
your equation becomes y = -8/144 * x^2 + 384/144 * x - 3456/144
that's the equation you see in the graph.

RELATED QUESTIONS
An engineer designs a parabolic arch to support a bridge with a two-lane road underneath... (answered by ikleyn)

a concrete bridge is designed with an arch in the shape of the parabola. The road over... (answered by josgarithmetic,MathTherapy)

The arch of a bridge over a two lane highway is in the shape of a semi-ellipse. The... (answered by Alan3354)

You live near a bridge that goes over a river. The underneath side of the bridge is an... (answered by Alan3354)

To obtain maximum strength engineers often design tunnels as parabolic arches. In such a (answered by stanbon,josgarithmetic)

A railway bridge over a ravine is supported by arches. The function that describes the... (answered by ankor@dixie-net.com)

A railroad bridge in one city has a low clearance for trucks. An Engineer standing 21 ft... (answered by ikleyn)

the sydney harbour bridge has its main steel arch in the shape of a parabola. The longest (answered by DrBeeee)

A bridge uses a parabolic arch to support it as shown in the picture. The bridge is 100 m (answered by galactus)