SOLUTION: how do i analyze a rational function?

Algebra ->  Rational-functions -> SOLUTION: how do i analyze a rational function?       Log On


   

Question 985083: how do i analyze a rational function?


Found 2 solutions by Alan3354, MathLover1:
Answer by Alan3354(69443) About Me  (Show Source):
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
Analyzing the graph of a rational function
step 1: Find the domain of the rational function
step 2: Write R in lowest terms (simplify the rational function if possible)
step 3: Locate the intercepts of the graph.
step 4: Test for symmetry
step 5: Locate the vertical asymptotes
step 6: Locate the horizontal or oblique asymptotes
step 7: Determine points, if any, where the graph crosses the asymptotes
(horizontal or oblique)
here is an example:

analyze the graph of a rational function

R%28x%29=%28x-1%29%2F%28x%5E2-4%29
step 1: Find the domain of the rational function
domain is:
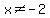
{ x| x%3C%3E2 and x%3C%3E-2
step 2: Write R in lowest terms (simplify the rational function if possible)
R%28x%29=%28x-1%29%2F%28%28x%2B2%29%28x-2%29%29+

step 3: Locate the intercepts of the graph.

R%280%29=%280-1%29%2F%28%280%2B2%29%280-2%29%29+
R%280%29=%28-1%29%2F%282%28-2%29%29+
R%280%29=%28-1%29%2F%28-4%29+
R%280%29=1%2F4+-> y-intercept is at (0,1%2F4)

0=%28x-1%29%2F%28%28x%2B2%29%28x-2%29%29+
0%28%28x%2B2%29%28x-2%29%29+=%28x-1%29+
0+=x-1
x=1-> x-intercept is at (1,0)
step 4: Test for symmetry
if R%28-x%29+=+R%28x%29 the function has symmetry about the y­-axis
find R%28-x%29
R%28-x%29=%28-x-1%29%2F%28%28-x%29%5E2-4%29
R%28-x%29=-%28x%2B1%29%2F%28x%5E2-4%29+
so, R%28-x%29+%3C+%3E+R%28x%29 => no symmetry
and R%28-x%29%3C%3E-R%28x%29, the function has no symmetry about the origin

step 5: Locate the vertical asympthote
%28x%2B2%29%28x-2%29=0=>x=2 and x=-2 are the vertical asympthotes
for next step:
Horizontal and Oblique Asympthote reminder(the degree of the numerator is n
and the degree of the denominator is m)
1.
If n+%3C+m, then R is a proper fraction and will have the horizontal asympthote y+=+0.
2.
If n+%3Em, then R is improper and long division is used.
(a)
If n+=+m, the quotient obtained will be a number, and the line y = is a horizontal asymptote.
(b)
If n+=+m+%2B+1, the quotient obtained is of the form ax+%2B+b(a polynomial of degree 1), and the line y+=+ax+%2B+b is an oblique asymptote.
(c)
If+n+%3E+m+%2B+1, the quotient obtained is a polynomial of degree 2 or higher and R has
neither a horizontal nor an oblique asymptote.
Horizontal asymptote:
%28x-1%29%2F%28%28x-2%29+%28x%2B2%29%29-%3E0 as x->±infinity
so, horizontal asymptote is y=0
no oblique asymptotes found
step 7: Determine points, if any, where the graph crosses the asymptotes
x-1=0
x=1
0=%28x-1%29%2F%28%28x-2%29+%28x%2B2%29%29
graph: