SOLUTION: find the equation describing all points equidistant from the x-axis and the point (0,2)

Algebra ->  Rational-functions -> SOLUTION: find the equation describing all points equidistant from the x-axis and the point (0,2)       Log On


   

Question 1137032: find the equation describing all points equidistant from the x-axis and the point (0,2)
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
find an equation describing all points equidistant from the x-axis and the point (0, 2).
First, see if you can sketch a picture of what this curve ought to look like.
For a point (x, y) that is on the curve, explain why sqrt%28y%5E2%29=+sqrt%28x%5E2+-+%28y+-+2%29%5E2%29.
note:
sqrt%28y%5E2%29 is the distance from (x, y) to the x-axis
sqrt%28x%5E2+-+%28y+-+2%29%5E2%29 is the distance from (x, y) to the point (0, 2)
distances must be equal because is given:all points equidistant from the x-axis and the point (0,2)

Square both sides of this equation and solve for+y. Identify the curve.
y%5E2=+x%5E2+-+%28y+-+2%29%5E2
y%5E2=+x%5E2+-+%28y%5E2+-+4y%2B4%29
y%5E2=+x%5E2+-+y%5E2+%2B4y-4
2y%5E2-4y=+x%5E2++-4......complete square for y
2%28y%5E2-2y%2Bb%5E2%29-2b%5E2=+x%5E2++-4
2%28y%5E2-2y%2B1%5E2%29-2%2A1%5E2=+x%5E2++-4
2%28y-1%29%5E2-2=+x%5E2++-4
2%28y-1%29%5E2=+x%5E2++-4%2B2
%28y-1%29%5E2=+%28x%5E2++-2%29%2F2
y=+sqrt%28x%5E2%2F2++-1%29%2B1=>hyperbola



Answer by ikleyn(52793) About Me  (Show Source):
You can put this solution on YOUR website!
.

            The solution by @MathLover1 is incorrect.

            It is incorrect,  because the formula for the distance from the point (0,2) to the point  (x,y) is   sqrt%28x%5E2+%2B+%28y-2%29%5E2%29,  and not   sqrt%28x%5E2+-+%28y-2%29%5E2%29.

            The final curve should be a parabola,  not a hyperbola.

            I know it very well,  since I solved similar problems several times at this forum.

            The correct solution is below.


Solution 

The distance from  (x, y) to the x-axis is  |y|.

 
The distance from   (x, y) to the point (0, 2) is  sqrt%28x%5E2+%2B+%28y+-+2%29%5E2%29.


The base equation is


|y| = sqrt%28x%5E2+%2B+%28y+-+2%29%5E2%29.


Square both sides of this equation and solve for+y.  

y%5E2 = x%5E2+%2B+%28y+-+2%29%5E2

y%5E2 = x%5E2+%2B+%28y%5E2+-+4y%2B4%29

0 = x%5E2+-+4y+%2B+4

4y =  x%5E2+%2B+4

y = %281%2F4%29%2Ax%5E2+%2B+1    <==========>  parabola with the branches upward; the vertex at the point (0,1)



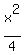    graph+%28+400%2C+400%2C+-10%2C+10%2C+-5%2C+10%2C%0D%0A+++++++++++++x%5E2%2F4+%2B+1%0D%0A%29


                Plot  y = x%5E2%2F4 + 1