Question 1100994: What does the degree of a polynomial expression tell you about its related polynomial function? Explain your thinking. Give an example of a polynomial expression of degree three. Provide information regarding the graph and zeros of the related polynomial function.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! WHAT COULD YOU BE EXPECTED TO BE THINKING?
Maybe you are expected to think like a calculus/pre-calculus student:
The end behavior of a polynomial function of even degree
can be represented by this  or or  . .
The graph of function like that may may never cross the x-axis,
so the function could have no real zeros.
If it does have zeros, they will come in pairs,
because "what goes up must come down" and vice versa.
Of course the function cannot have more zeros than its degree.
For example, a polynomial function of degree 6 could have 0, 2, 4, or 6 real zeros.
The end behavior of a polynomial function of even degree
can be represented by this  or or  . .
The graph of function like that must cross the x-axis at least once,
so the function must have at least one real zero.
There and be up to as many real zeros as the degree of the polynomial function , and there will be an odd number of real zeros,
because an even number would mean an end-behavior like the one described by even degree polynomial functions.
Maybe you are expected to think in terms of polynomial factoring:
A polynomial of degree  must have must have  complex number zeros, complex number zeros,
and could be written as
 , where , where  is the leading coefficient. is the leading coefficient.
Some of those complex number zeros may not be real numbers,
but those will come as  pairs of conjugate complex number zeros, pairs of conjugate complex number zeros,
and in that case, a polynomial function with real coefficients can be written as
 where where 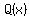 is a polynomial of degree is a polynomial of degree  with no real zeros. with no real zeros.
An example of a polynomial function of degree 3 is

It has 3 real zeros:  , ,  and and  . .
For  all 3 factors are positive and so is the function. all 3 factors are positive and so is the function.
Between  and and  , ,  is negative, is negative,
but the other two factors are positive, so the function is negative.
Between  and and  (for (for  ), ),
two factors are negative ,  and and  , ,
but the other factor is positive,  , and the function is positive. , and the function is positive.
For  , all three factors are negative, and so is the function. , all three factors are negative, and so is the function.

|
|
|