Working alone, it takes Heather 13 hours to tar a roof. Lea can tar the same roof in 15 hours. If they worked together how long would it take them?
The answer is 6.96 hours (I looked at the answer sheet! Shhh!), but I need to know how to solve it! And i have to show all of my work!
Help? Thank you so MUCH!!!
Make this chart:
|Number of roofs tarred |Time required |Rate in roofs/hr
Heather working alone | | |
Lea working alone | | |
Both working together | | |
Working alone, it takes Heather 13 hours to tar 1 roof
Therefore fill in 13 hours for her time, and 1 for the number of roofs tarred.
|Number of roofs tarred |Time required |Rate in roofs/hr
Heather working alone | 1 | 13 |
Lea working alone | | |
Both working together | | |
Lea can tar the same roof in 15 hours
Therefore fill in 15 for her time, and 1 for the number of roofs tarred.
|Number of roofs tarred |Time required |Rate in roofs/hr
Heather working alone | 1 | 13 |
Lea working alone | 1 | 15 |
Both working together | | |
Fill in x for the time required for both working together, and 1 for the
number of roofs tarred.
|Number of roofs tarred |Time required |Rate in roofs/hr
Heather working alone | 1 | 13 |
Lea working alone | 1 | 15 |
Both working together | 1 | x |
Finish filling in the chart by using


 |Number of roofs tarred |Time required |Rate in roofs/hr
Heather working alone | 1 | 13 | 1/13
Lea working alone | 1 | 15 | 1/15
Both working together | 1 | x | 1/x
Form the equation from:
{Heather's rate} + (Lea's rate) = (Rate of Both working together)
|Number of roofs tarred |Time required |Rate in roofs/hr
Heather working alone | 1 | 13 | 1/13
Lea working alone | 1 | 15 | 1/15
Both working together | 1 | x | 1/x
Form the equation from:
{Heather's rate} + (Lea's rate) = (Rate of Both working together)

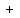
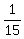

 Solve that and get
Solve that and get  which does come out to 6.964285714
Edwin
which does come out to 6.964285714
Edwin