SOLUTION: In mowing the backyard lawn, it takes James and his btoher , Chris each with his mower , 3 hours and 20 minutes to do the job . Working alone, Chris would need 5 hours longer than

Algebra ->  Rate-of-work-word-problems -> SOLUTION: In mowing the backyard lawn, it takes James and his btoher , Chris each with his mower , 3 hours and 20 minutes to do the job . Working alone, Chris would need 5 hours longer than       Log On


   

Question 1087909: In mowing the backyard lawn, it takes James and his btoher , Chris each with his mower , 3 hours and 20 minutes to do the job . Working alone, Chris would need 5 hours longer than James to finish the job . How long would it take each of them alone to do the job
Found 2 solutions by ankor@dixie-net.com, ikleyn:
Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
In mowing the backyard lawn, it takes James and his btoher , Chris each with his mower , 3 hours and 20 minutes to do the job .
Working alone, Chris would need 5 hours longer than James to finish the job .
How long would it take each of them alone to do the job
:
Use 3.33 hrs for 3 hrs and 20 min
:
let = time required by J working alone
then
(t+5) = time for C working alone
let the completed job = 1
:
A typical shared work equation
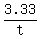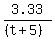3.33%2Ft + 3.33%2F%28%28t%2B5%29%29 = 1
multiply by t(t+5).cancel the denominators
3.33(t+5) + 3.33t = t(t+5)
3.33t + 16.67 + 3.33t = t^2 + 5t
6.66t + 16.67 = t^2 + 5t
a quadratic equation
0 = t^2 + 5t - 6.67t - 16.67
t^2 - 1.67t - 16.67 = 0
using the quadratic formula, I got a positive solution of:
t = 5 hrs is J's time alone
then
5 + 5 = 10 hrs is C's time alone

Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let x be the time for James to make the job working alone.

Then that of Chris is (x+5) hours.


James' rate of work is 1%2Fx of the job per hour.

Chris' rate of work is 1%2F%28x%2B5%29 of the job per hour.


Their combined  rate of work is  1%2Fx+%2B+1%2F%28x%2B5%29 of the job per hour.

And the condition says that it is 1%2F%28%2810%2F3%29%29 of the job per hour  ( 3 hours and 20 minutes = 10%2F3 of an hour).


It gives you an equation

1%2Fx+%2B+1%2F%28x%2B5%29 = 1%2F%28%2810%2F3%29%29,   or, which is the same,

1%2Fx+%2B+1%2F%28x%2B5%29 = 3%2F10.


To solve it, multiply both sides  by 10*x*(x+5). You will get

10*(x+5) + 10x = 3x*(x+5).


Solve this quadratic equation to get the

Answer. Time for James is 5 hours; times for Chris is 10 hours.


It is a typical joint work problem.

There is a bunch of similar solved joint-work problems/samples with detailed explanations in this site. See the lessons
    - Using Fractions to solve word problems on joint work
    - Solving more complicated word problems on joint work
    - Using quadratic equations to solve word problems on joint work (*)
and especially the lesson marked (*) as the most closest to your problem.


Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this textbook under the topic "Rate of work and joint work problems" of the section "Word problems".