SOLUTION: Jack and Jill can mow the park together in 10 hours. Jack and Joe can mow the same park together in 15 hours. jill and Joe can mow the same park together in 18 hours. Determine the

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Jack and Jill can mow the park together in 10 hours. Jack and Joe can mow the same park together in 15 hours. jill and Joe can mow the same park together in 18 hours. Determine the      Log On


   

Question 1055380: Jack and Jill can mow the park together in 10 hours. Jack and Joe can mow the same park together in 15 hours. jill and Joe can mow the same park together in 18 hours. Determine the number of hours it would take jill alone to mow the park. Express your answer as a common fraction reduced to lowest terms.
Found 2 solutions by josmiceli, ikleyn:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
[ rate of mowing ] = [ 1 park mowed ] / [ t hrs ]
[ rate of mowing ] = [ R ]
+R%5Ba%5D+ = Jack's rate of mowing
+R%5Bb%5D+ = Jill's rate of mowing
+R%5Bc%5D+ = Joe's rate of mowing
--------------------------------
Add rates of mowing to get the rate mowing together
(1) +R%5Ba%5D+%2B+R%5Bb%5D+=+1%2F10+
(2) +R%5Ba%5D+%2B+R%5Bc%5D+=+1%2F15+
(3) +R%5Bb%5D+%2B+R%5Bc%5D+=+1%2F18+
--------------------------------
Add (1) and (3) and subtract (2)
+R%5Ba%5D+%2B+2R%5Bb%5D+%2B+R%5Bc%5D+=+1%2F10+%2B+1%2F18+
+-R%5Ba%5D+-+R%5Bc%5D+=+-1%2F15+
-------------------------------------
+2R%5Bb%5D+=+1%2F10+%2B+1%2F18+-+1%2F15+
+R%5Bb%5D+=+1%2F20+%2B+1%2F36+-+1%2F30+
+R%5Bb%5D+=+9%2F180+%2B+5%2F180+-+6%2F180+
+R%5Bb%5D+=+8%2F180+
+R%5Bb%5D+=+2%2F45+
+R%5Bb%5D+=+1%2F%28%28+45%2F2+%29%29+
( This is [ 1 park mowed ] / [ 45/2 hrs ] )
--------------------------------------------
It will take Jill 45/2 hrs to mow the park alone
--------------------------------------------
check answer:
(1) +R%5Ba%5D+%2B+R%5Bb%5D+=+1%2F10+
(1) +R%5Ba%5D+%2B+2%2F45+=+1%2F10+
(1) +R%5Ba%5D+=+9%2F90+-+4%2F90+
(1) +R%5Ba%5D+=+5%2F90+
(1) +R%5Ba%5D+=+1%2F18+
and
(3) +R%5Bb%5D+%2B+R%5Bc%5D+=+1%2F18+
(3) +2%2F45+%2B+R%5Bc%5D+=+1%2F18+
(3) +R%5Bc%5D+=+5%2F90+-+4%2F90+
(3) +R%5Bc%5D+=+1%2F90+
-----------------------------
(2) +R%5Ba%5D+%2B+R%5Bc%5D+=+1%2F15+
(2) +1%2F18+%2B+1%2F90+=+1%2F15+
(2) +5%2F90+%2B+1%2F90+=+6%2F90+
-----------------------------
(1) +R%5Ba%5D+%2B+R%5Bb%5D+=+1%2F10+
(1) +1%2F18+%2B+2%2F45+=+1%2F10+
(1) +5%2F90+%2B+4%2F90+=+9%2F90+
-----------------------------
(3) +R%5Bb%5D+%2B+R%5Bc%5D+=+1%2F18+
(3) +2%2F45+%2B+1%2F90+=+1%2F18+
(3) +4%2F90+%2B+1%2F90+=+5%2F90+
-----------------------------
OK



Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
Jack and Jill can mow the park together in 10 hours.
Jack and Joe can mow the same park together in 15 hours.
Jill and Joe can mow the same park together in 18 hours.
Determine the number of hours it would take Jill alone to mow the park.
Express your answer as a common fraction reduced to lowest terms.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

There is more short and elegant method to solve this problem. 

Let "a", "b" and "c" be the rate-of-work of each of the persons Jack, Jill, and Joe, respectively.

We are given that 

a + b = 1%2F10,    (1)
a + c = 1%2F15,    (2)
b + c = 1%2F18.    (3)

To solve the system (1), (2), (3), let us start adding the equations (1), (2) and (3). You will get 

2a + 2b + 2c = 1%2F10+%2B+1%2F15+%2B+1%2F18 = 9%2F90+%2B+6%2F90+%2B+5%2F90 = %289%2B6%2B5%29%2F90 = 20%2F90 = 2%2F9.

Hence, 

a + b + c = 1%2F9.

Thus we just found the combined rate-of-work of the three persons working together. It is 1%2F9 job per hour.

Now, whose productivity we must to estimate? Jill's alone?
Distract the equation (2) from (4). You will get

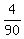b = 1%2F9+-+1%2F15 = 10%2F90+-+6%2F90 = 4%2F90 = 2%2F45.

It means that Jill alone can mow 2%2F45 of the area per hour.
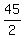Hence, it will take  45%2F2 = 22.5 hours for Jill to mow the park working alone.

Answer.  It will take  22.5 hours for Jill to mow the park working alone.

Solved.

See also the lesson
    - Joint-work problems for 3 participants, Problem 2
in this site.

Very similar problem was solved there using the same method.


Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this textbook under the topic "Rate of work and joint work problems" of the section "Word problems".