Question 61942: i really need help with this but no one has responded...is there anyone who can help? PLEASE!
fireworks are launched into the air. the quadratic function that models the fireworks height, s(x), in feet, x seconds after they are launched is given by the equation s(x)=-16x^2+200x+4. when should the fireworks explode so that they go off at the greatest height? What is that height?
Found 3 solutions by stanbon, ankor@dixie-net.com, Earlsdon:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! s(x)=-16x^2+200x+4. when should the fireworks explode so that they go off at the greatest height? What is that height?
--------------
You have a quadratic with a=-16 and b=200
The maximum point occurs at x=-b/2a=-200/(-32)=6.25 seconds
The height at that time is
s(6.25)=629 ft.
Cheers,
Stan H.
Answer by ankor@dixie-net.com(22740)  (Show Source):
You can put this solution on YOUR website! fireworks are launched into the air. the quadratic function that models the fireworks height, s(x), in feet, x seconds after they are launched is given by the equation s(x)=-16x^2+200x+4. when should the fireworks explode so that they go off at the greatest height? What is that height?
:
This is an ordinary quadratic equation so finding the vertex will give you the value of x when the maximum height is obtained.
:
The vertex formula: x = -b/(2*a)
:
In your equation a = -16; b = +200
:
x = -200/(2*-16)
x = -200/-32
x = +6.25 seconds after launch the firework should explode
:
To find the actual height of the maximum, substitute 6.25 for x in the original equation:
s(x) = -16(6.25^2) + 200(6.25) + 4
s(x) = -16(39.0625) + 1250
s(x) = -625 + 1250
s(x) = +625 ft is the max height and occurs after 6.25 sec
:
A graphical presentation would help you understand it
Answer by Earlsdon(6294) (Show Source):
You can put this solution on YOUR website! The function that relates the height, h, (in feet) of an object propelled upwards as a function of time, t, (in seconds) is given by:
 where: Vo is the initial upward velocity and Ho is the initial height of the object.
When graphed, the given quadratic equation will yield a parabola that opens downward. So to answer the question, you will need to find the maximum value of the function s(x).
The maximum value is at the vertex of the parabola and this is given by 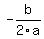 . The a and b come from the general form of the quadratic equation:  .
In this problem, a = -16 and b= 200, so the x-coordinate of the vertex is:
The maximum height reached by the firework is attained at time, t = 6.25 seconds and that is when the explosion should occur.
To find the height at t = 6.25 seconds, substitute t = 6.25 into the quadratic equation and solve for s.
 feet.
|
|
|
