SOLUTION: which quadratic equations has roots of -3 and 2?

Algebra.Com
Question 1156388: which quadratic equations has roots of -3 and 2?

Found 3 solutions by MathLover1, ikleyn, Theo:
Answer by MathLover1(20849)   (Show Source): You can put this solution on YOUR website!
roots of and










Answer by ikleyn(52781)   (Show Source): You can put this solution on YOUR website!
.

Any quadratic equation of the form


   a*(x-(-3))*(x-2) = 0,


which is the same as 


    a*(x+3)*(x-2) = 0,


where "a" is any non-zero real number.


There are INFINITELY MANY such equations.


And they ALL are EQUIVALENT, i.e. have the same set of solutions.


Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
the roots are -3 and 2
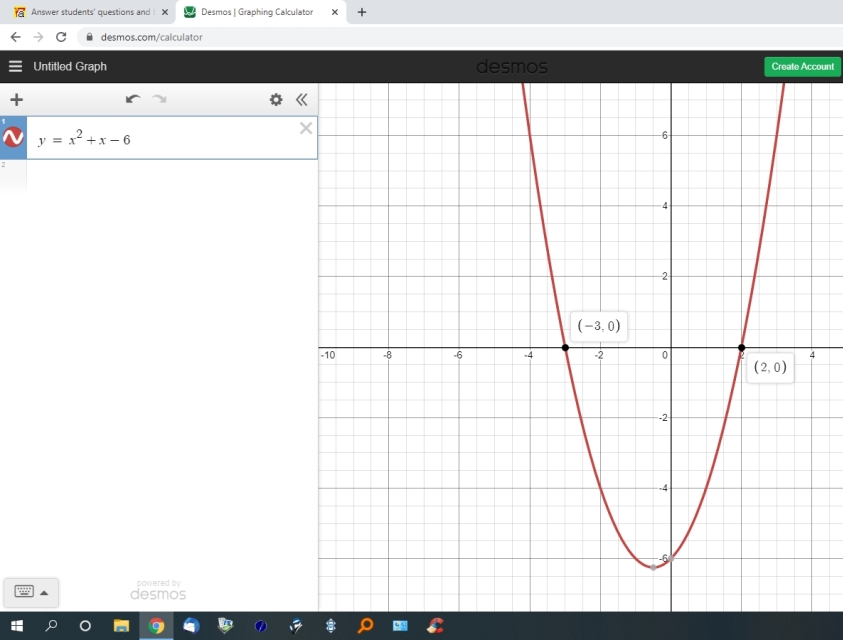
set x = -3
add 3 to both sides of that equation to get x + 3 = 0
that's one of your factors.
set x = 2
subtract 2 from both both sides of that equation to get x - 2 = 0
that's your other factor.
your factors are (x + 3) * (x - 2) = 0
simplify that equation to get x^2 - 2x + 3x - 6 = 0
combine like terms to get x^2 + x - 6 = 0
the graph of that equation looks like this.

$$$
RELATED QUESTIONS

Which quadratic equation has roots 7 and... (answered by solver91311)
Which quadratic equation has roots -2 and... (answered by Fombitz)
Which quadratic equation has roots -2 and... (answered by Fombitz)
Which Of The following equations has roots Of -3/2 and... (answered by solver91311)
which quadratic equation has the roots 2-radical 3 and 2 + radical 3? (answered by lwsshak3)
Which quadratic equation has roots -2 and... (answered by solver91311)
If the roots of a quadratic equation are -3 and 1/2 find the... (answered by Alan3354)
find the quadratic equation which has difference of roots equal to 2 and the difference... (answered by ikleyn)
write the quadratic equation which has 7 and -3 as its... (answered by Edwin McCravy)