Question 1104242: Find the product (xy) if x+y+ = 20 and x-y+ = 20 and x-y+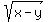 =12. =12.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is assumed in the given equations that 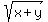 >= 0 and >= 0 and 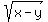 >= 0.
1. Let u = >= 0.
1. Let u = 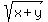 . Then . Then
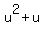 = 20, or = 20, or
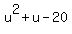 = 0.
Factor left side
(u+5)*(u-4) = 0.
As just noticed above, = 0.
Factor left side
(u+5)*(u-4) = 0.
As just noticed above, 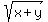 assumed to be >= 0.
Therefore, only positive root u = 4 works.
Thus, assumed to be >= 0.
Therefore, only positive root u = 4 works.
Thus, 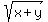 = 4. Then x + y = 4^2 = 16.
2. Similarly, Let v = = 4. Then x + y = 4^2 = 16.
2. Similarly, Let v = 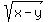 . Then . Then
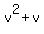 = 12, or = 12, or
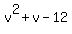 = 0.
Factor left side
(v+4)*(v-3) = 0.
As just noticed above, = 0.
Factor left side
(v+4)*(v-3) = 0.
As just noticed above, 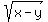 assumed to be >= 0.
Therefore, only positive root v = 3 works.
Thus, assumed to be >= 0.
Therefore, only positive root v = 3 works.
Thus, 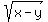 = 3. Then x - y = 3^2 = 9.
3. Thus we have two equations
x + y = 16,
x - y = 9,
which implies x= 12.5, y= 3.5.
Answer. The solution is x= 12.5, y= 3.5. The product xy = 43.75. = 3. Then x - y = 3^2 = 9.
3. Thus we have two equations
x + y = 16,
x - y = 9,
which implies x= 12.5, y= 3.5.
Answer. The solution is x= 12.5, y= 3.5. The product xy = 43.75.
Solved.
Answer by greenestamps(13203)   (Show Source): (Show Source):
|
|
|