|
Question 979420: A parabolic arch must have a clearance of 40 ft above the water and a
span distance of 160 ft.
(a) Find an equation which models this shape, using the x-axis to represent the water ground.
(b) Find the height from the base of the arch spanning 20 ft.
Found 2 solutions by solver91311, josgarithmetic:
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website!
There are a couple of ways to set this up that make sense. Making the  -axis be the axis of symmetry keeps everything symmetrical or you could put one of the end-points of the arch at the origin allowing you to use the origin as one of the three points that define the parabola.
Let's use the -axis as the parabola axis, meaning that the -axis passes through the vertex of the parabola. We are given that the function value at the vertex is 40 feet, so we now have the point ) as one of the points on the desired parabola.
Since the base of the arch must span 160 feet, and we have placed the center of the base at the origin, the ends of the arch must be 80 feet on either side of the origin. Hence, our other two points are ) and )
Now that we have three points, we can proceed to find the function for which the graph passes through them.
The standard form equation of a parabolic function is:
\ =\ ax^2\ +\ bx\ +\ c)
Recall that the ordered pair describing a point on the graph of a function is \right)) .
Hence, if the point is a point on the desired function then the following relationship must hold:
^2\ +\ b(-80)\ +\ c\ =\ 0)
Likewise, for )
^2\ +\ b(80)\ +\ c\ =\ 0)
and for )
^2\ +\ b(0)\ +\ c\ =\ 40)
Giving rise to the 3X3 linear system:
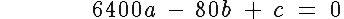
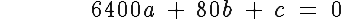
Now all you have to do is solve the 3X3 system to find the coefficients of the desired function.
You could also choose to use the points ) , ) and ) . In fact, you could chose any two points on the  -axis and an appropriate vertex and get a correct result -- if you are some kind of masochist that enjoys doing ugly arithmetic.
John
My calculator said it, I believe it, that settles it
Answer by josgarithmetic(39621)  (Show Source):
|
|
|
| |
