



 is the equation of a hyperbola like this " )( "
with center (h,k), semi-transverse axis = a, semi-conjugate axis = b
is the equation of a hyperbola like this " )( "
with center (h,k), semi-transverse axis = a, semi-conjugate axis = b


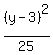






 We
1. Plot the center (2,3).
2. Draw the transverse axis (red) of 2a = 2(6) = 12
3. Draw the conjugate axis (blue) of 2b = 2(5) = 10,
4. defining rectangle (in green)
5. Draw and extend diagonals forming asymptotes (dotted lines),
6. Sketch the hyperbola.
7. Calculate c by c²=a²+b²=36+25=61, c=
We
1. Plot the center (2,3).
2. Draw the transverse axis (red) of 2a = 2(6) = 12
3. Draw the conjugate axis (blue) of 2b = 2(5) = 10,
4. defining rectangle (in green)
5. Draw and extend diagonals forming asymptotes (dotted lines),
6. Sketch the hyperbola.
7. Calculate c by c²=a²+b²=36+25=61, c= 8. Foci are (h±c,k) which are (2-
8. Foci are (h±c,k) which are (2- ,3), (2+
,3), (2+ ,3), the big black dots.
9. Find equations of asymptotes. Slopes are
,3), the big black dots.
9. Find equations of asymptotes. Slopes are 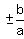 through (h,k)
Slopes are (((""+-5/6}}} through (2,3)
Use point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = (2,3)
y - 3 =
through (h,k)
Slopes are (((""+-5/6}}} through (2,3)
Use point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = (2,3)
y - 3 =  (x - 2) and y - 3 =
(x - 2) and y - 3 = 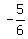 (x - 2)
You can simplify those equations.
(x - 2)
You can simplify those equations.
 Edwin
Edwin