|
Question 855915: write the equation of the parabola with vertex at the origin which satisfies the given condition:
a.axis on the y-axis and passes through (6,-3)
b.focus (0,4/3) and the equation of the directrix is y+4/3=0
c.directrix is x-4=0
d.focus at(0,2)
e. latus rectum is 6 units and the parabola opens to the left
f.focus on the x-axis and passes through (4,3)
ive tried answering but i dont know if i got the ryt answers . can anybody help me ? thank u so much in advance god bless
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Equation of the parabola with vertex at the origin which satisfies the given condition:
a. axis on the y-axis and passes through (6,-3)
Since the axis is on the y-axis, the equation is of the form  .
We just have to find the constant  .
Since it passes through the point with  and  ,
 --> --> --> .
So the equation is  or  .
b. focus (0,4/3) and the equation of the directrix is y+4/3=0
That is twice as much information as needed.
We do not need both directrix and focus when we already have the vertex.
The focus and directrix must be at the same distance from the vertex,
so knowing that the vertex is at (0,0),
if the focus is at (0,4/3) the directrix equation had to be  <--> .
In a parabola with a focal distance of  the absolute value of the coefficient of the squared term is  .
Since the focus has the same x-coordinate as the vertex, which is the origin,
and the focus has a positive y-coordinate,
the rest of the parabola is also above the x-axis.
So the coefficient is positive, and the equation is
 --> .
c. directrix is x-4=0
 <--> , meaning that the focal distance is  ,
and that the directrix is to the right of the vertex (the origin).
That means that the focus and the parabola (except for the vertex) are to the left of the y-axis.
Then the equation must be
 --> --> .
d. focus at(0,2)
That means the focal distance is  and the focus is above the (0,0) vertex.
The equation of the parabola is
 --> .
e. latus rectum is 6 units and the parabola opens to the left.
With the vertex at the origin and the parabola opening to the left, the equation is
 with a negative coefficient,  .
with the focal distance represented by , the latus rectum length is 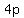 and the absolute value of the coefficient is , the reciprocal of the latus rectum length.
So the equation is
|
|
|
| |
