|
Question 65288: If the eccentricity of an ellipse (in other words, the value e) is close to zero, then the ellipse looks almost like a circle.
True
False
Each of the remaining questions refer to the ellipse 4x^ 2 + 9y ^2 - 8x + 36y + 4 = 0.
The center of the ellipse is at the point
(-1,2)
(-2,1)
(1,-2)
(2,-1)
The foci of the ellipse are the points
The length of the major axis of the ellipse is
6 units
3 units
4 units
2 units
The length of the minor axis is
3 units
6 units
4 units
2 units
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1). The eccentricity of an ellipe is given by:
 Where c is the distance of the foci from the centre of the ellipse and a is half the length of the major axis. If c is close to zero, the foci are close to the centre and, therefore, the ellipse is close to being a circle. Where c is the distance of the foci from the centre of the ellipse and a is half the length of the major axis. If c is close to zero, the foci are close to the centre and, therefore, the ellipse is close to being a circle.
2). Given the equation of the ellipse:
 , find the coordinates of the centre, the length of the major axis, and the length of the minor axis. , find the coordinates of the centre, the length of the major axis, and the length of the minor axis.
To find these you should get your equation into the standard form for an ellipse with its centre at (h, k), semi-major axis = a and semi-minor axis = b.
 and to do this you will need to use the process of "completing the square". But first rearrange your equation as follows: and to do this you will need to use the process of "completing the square". But first rearrange your equation as follows:
 Subtract 4 from both sides. Subtract 4 from both sides.
 Now complete the squares in the x-terms and in the y-terms by making the coefficients of the Now complete the squares in the x-terms and in the y-terms by making the coefficients of the  and the and the  term equal to 1. You can do this by dividing through by LCD of 36. term equal to 1. You can do this by dividing through by LCD of 36.
 Now cancel where appropriate. Now cancel where appropriate.
 Now complete the squares in the x-terms and the y-terms by adding Now complete the squares in the x-terms and the y-terms by adding  and and 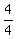 respectively to both sides of the equation. respectively to both sides of the equation.
 Simplifying this, you get. Simplifying this, you get.
 Compare this with the standard form: Compare this with the standard form:
 with centre at (h, k), a = 3 and b = 2 with centre at (h, k), a = 3 and b = 2
So the centre of the ellipse is at: (1, -2)
The foci are located on the major axis at c units from the centre, where:



The major axis is parallel to the x-axis, so the foci are located at:
(1+sqrt(13), -2) and (1-sqrt(13), -2)
The length of the major axis is 2a = 2(3) = 6.
The length of the minor axis is 2b = 2(2) = 4.
|
|
|
| |